1

I need a mathematical solution to a very practical problem (laying a patio).

The attached will hopefully explain.

The center of the circle for the arc we wish to have is inaccessible (ie in the house behind walls).

There are 2 fixed points the arc must intersect.

There is an existing arc drawn using these 2 fixed points, but this circle is too small - radius 539cm

The desired arc is more shallow so would have a greater radius.

I think I need 10 or so measurements from the center of this existing circle, to the new arc.

These points can then be plotted on the ground and the dots joined up (obviously more than 10 will me more accurate, but 10 seems a sensible number)

I am sure this is possible, but my mathematical knowledge is not good enough, sorry. Answers or a simple formula I can apply would be very much appreciated.

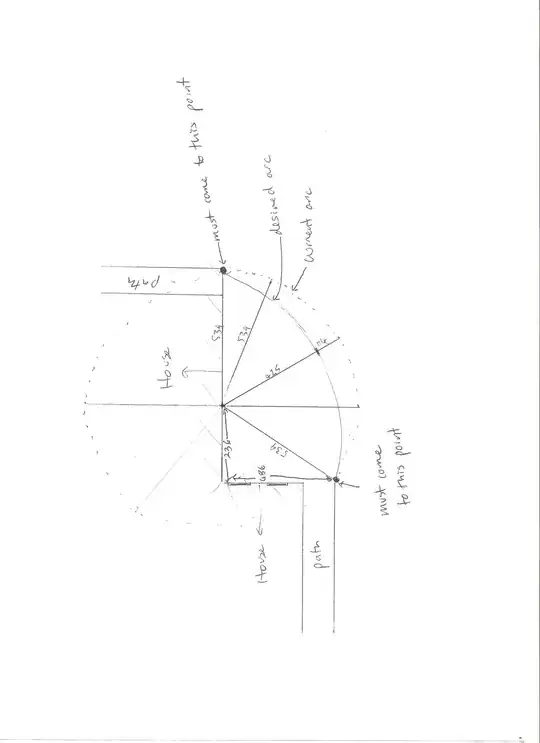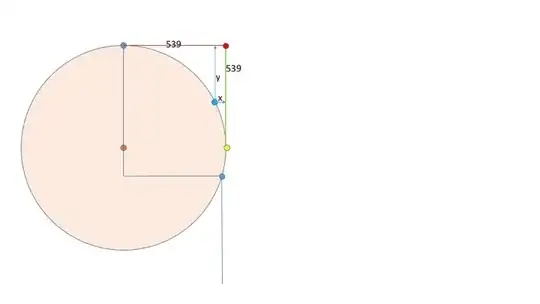
enter image description here Anyone out there to help?

J. M. ain't a mathematician
  • 76,540
claret
  • 21
  • The problem, as stated, has infinitely many solutions. Knowing two points of an arc does not determine the arc. If you ALSO know a line along which the center must lie (like the long horizontal line near the letter "H" in "House" in your drawing), then we can help you. Or if you say that the tangent line at one of the points must point in a certain direction...THEN we can help you. Without that...there's not enough information. – John Hughes Jun 30 '16 at 11:21
  • Thank you John. (I'm sorry, my comparative stupidity on this subject must irritate users of the forum) I appreciate your help so far. The center should lie on the line labelled 425. That is the point of maximum distance between the existing arc and desired arc. – claret Jun 30 '16 at 11:30
  • Doesn't irritate us at all (at least not me). But we do often use the comments to help askers clarify their questions, as in this example. I'll write up a solution shortly. – John Hughes Jun 30 '16 at 11:54
  • I was mistaken in what I said earlier: two points and a line containing the center isn't enough. But from your drawing, it looks as if the top point (near the top of the drawing, labelled "must come to this point") is actually the top point of the circle, i.e., the tangent to the circle at that point is horizontal. Is that correct? If so, this is relatively easy. – John Hughes Jun 30 '16 at 12:10
  • This could be helpful: http://math.stackexchange.com/questions/862915/how-to-create-circles-and-or-sections-of-a-circle-when-the-centre-is-inaccessibl – user84976 Jun 30 '16 at 16:23

3 Answers3

1

enter image description here

In the picture above, I've drawn in the circle that I think you want, drawing it as a large pale-orange disk. The blue zig-zag line corresponds to the line in your figure, and the blue dots are the two points where you said the circle has to go. I'm making the assumption that the circle is supposed to have the top blue point as its uppermost point.

So here's what you do: extend the line of the upper walk 539 units to the right (the red segment) and mark a point there. That's the red dot in the picture. Notice that the green line coming down from it will NOT pass through the other blue point, so don't go trying to move things to make that happen ... it'll just make things wrong.

We're going to measure everything from this red point, either left-right (i.e., along the red segment) or up-down (along the green segment). It'll help if you actually draw a line parallel to the red one, but further down, and a line parallel to the green one, but further left, and fill in a kind of grid of chalk-lines or something to help guide you.

You want to find points on the circle arc like the aqua one. To help you do that, I'm going to give you "x" and "y" measurements, where "x" is "how far to the left of the green line" and $y$ is "how far down from the red line". They're computed like this:

$$ x = 539 (1 - \cos(t) ) \\ y = 539 (1 - \sin(t) ) $$

where $t$ is any number, and indicates the angle counterclockwise from horizontal (using a ray from the orange dot through the yellow one as a reference). Fortunately, you don't need to measure $t$. You just need a table, so I've appended it below. If you look about a third of the way down the table, you'll see a point $0, 539$. That means that if you go left from the red dot by 0 units, and down by 539 units, you've got a point on your circle....that's the yellow point in the figure!

To actually draw your curve, I'd take a few $x$ values that are all bigger than about 200 -- say 200, 250, 300, 350, 400, 450, 500 -- and use the table to find the corresponding $y$ values (or at least as near as you can come). That'd give me

199.7963  120.1183
253.3735   81.9021
302.7180   54.5500
354.6511   32.5057
408.6041   16.0106
454.6818    6.6360
501.4013    1.3130
539.0000         0

For each of these, I'd measure $x$ units to the left of the red dot, along the red line, and then $y$ units down. So for the first one, I'd measure 199.79 units to the left of the red dot, and then move down 120.12 units, and I'd draw a point. To be honest, I'd measure 200 to the left and 120 down, rounding off to the nearest whole number, because I'm figuring that these numbers are probably cm, and little bits don't matter a lot.

Then I'd do the same thing again, but this time I'd pick $y$ values between 200 and 700, something like this:

 26.3805  705.5602
 11.7784  651.0644
  4.0176  604.6876
  0.0821  548.4068
  1.3130  501.4013
  6.6360  454.6818
 18.3660  399.4965
 32.5057  354.6511
 54.5500  302.7180
 81.9021  253.3735
120.1183  199.7963

For each of these, I'd measure $y$ units down from the red dot, and then $x$ units to the left. For the third row, for instance, I'd measure 605 units down and then 4 units to the left, which would give me a point a little below and to the left of the yellow dot.

This collection of points should give you enough to let you draw in the rest of the curve by bending a long thin piece of wood around some pegs set in the ground, etc. --- I'm assuming you can do this part on your own.

Here's the table of all the values:

 72.2123  808.5000
 67.5800  800.3124
 63.0912  792.0452
 58.7475  783.7009
 54.5500  775.2820
 50.5001  766.7912
 46.5990  758.2311
 42.8479  749.6041
 39.2479  740.9130
 35.8002  732.1603
 32.5057  723.3489
 29.3655  714.4812
 26.3805  705.5602
 23.5517  696.5883
 20.8799  687.5685
 18.3660  678.5035
 16.0106  669.3959
 13.8145  660.2486
 11.7784  651.0644
  9.9029  641.8460
  8.1886  632.5964
  6.6360  623.3182
  5.2455  614.0143
  4.0176  604.6876
  2.9527  595.3408
  2.0511  585.9769
  1.3130  576.5987
  0.7387  567.2091
  0.3283  557.8108
  0.0821  548.4068
  0       539.0000
  0.0821  529.5932
  0.3283  520.1892
  0.7387  510.7909
  1.3130  501.4013 
  2.0511  492.0231
  2.9527  482.6592
  4.0176  473.3124
  5.2455  463.9857
  6.6360  454.6818
  8.1886  445.4036
  9.9029  436.1540
 11.7784  426.9356
 13.8145  417.7514
 16.0106  408.6041
 18.3660  399.4965
 20.8799  390.4315
 23.5517  381.4117
 26.3805  372.4398
 29.3655  363.5188
 32.5057  354.6511
 35.8002  345.8397
 39.2479  337.0870
 42.8479  328.3959
 46.5990  319.7689  
 50.5001  311.2088
 54.5500  302.7180
 58.7475  294.2991
 63.0912  285.9548
 67.5800  277.6876
 72.2123  269.5000
 76.9868  261.3945
 81.9021  253.3735
 86.9566  245.4396
 92.1487  237.5950
 97.4770  229.8423
102.9398  222.1837
108.5355  214.6217
114.2622  207.1585
120.1183  199.7963
126.1020  192.5375
132.2115  185.3842
138.4449  178.3386
144.8004  171.4029
151.2758  164.5791
157.8694  157.8694
164.5791  151.2758
171.4029  144.8004
178.3386  138.4449
185.3842  132.2115
192.5375  126.1020
199.7963  120.1183
207.1585  114.2622
214.6217  108.5355
222.1837  102.9398
229.8423   97.4770
237.5950   92.1487
245.4396   86.9566
253.3735   81.9021
261.3945   76.9868
269.5000   72.2123
277.6876   67.5800
285.9548   63.0912
294.2991   58.7475
302.7180   54.5500
311.2088   50.5001
319.7689   46.5990
328.3959   42.8479
337.0870   39.2479
345.8397   35.8002
354.6511   32.5057
363.5188   29.3655
372.4398   26.3805
381.4117   23.5517
390.4315   20.8799
399.4965   18.3660
408.6041   16.0106
417.7514   13.8145
426.9356   11.7784
436.1540    9.9029
445.4036    8.1886
454.6818    6.6360
463.9857    5.2455
473.3124    4.0176
482.6592    2.9527
492.0231    2.0511
501.4013    1.3130
510.7909    0.7387
520.1892    0.3283
529.5932    0.0821
539.0000         0
John Hughes
  • 100,827
  • 4
  • 86
  • 159
  • John - thank you also. I've worked through this, very easy to understand, and have been out and stringed and pegged it too. Brilliant. I really appreciate the time taken to present this. – claret Jun 30 '16 at 14:50
  • Delighted to help. Glad it seems to have worked out. Learning to express things clearly enough for them to be valuable to the question-asker is one of my goals as I answer questions here. – John Hughes Jun 30 '16 at 16:09
0

This is not a direct answer, but (maybe) a practical solution for your problem:

usually, in order to drawing a circle, you can keep one end of a rope in the center of the circle and turn around with the other end. In this case this is not possible because the center of the circle is inside the house.

Following your picture, I've drawn this: enter image description here

$C$ is the center of the circle inside the house, $A$ and $B$ are the 2 fixed points the arc (red colored) must intersect. As you are not able to draw the red arc, I propose to draw its symmetric, the dotted arc, and then take its symmetric.

So partically I propose:

1-Draw the line $AB$

2-Find the symmetric of the center $C$ respect to the segment $AB$. We will call it $C'$

3- Take a rope of length $R$ equal to the radius of the circle. Call one person to help you (we will call it Bill).

4-Fix one end of the rope in $C'$. Keep the other end then ask to Bill to walk with the rope along the segment $AB$, starting from $A$ to $B$.

5-Clearly the rope will be longer, so you will be able to get the rope double. Mark the extremity of the doubled rope.

6- You will obtain the desired arc.

Remark: maybe there are some others barrier which prevent my solution too.

user84976
  • 674
  • That is a excellent (elegant and practical) solution to my problem - thank you very much. Obvious when pointed out. It has worked perfectly, and one of the builders name's is Bill :-) Thank you once again. – claret Jun 30 '16 at 14:45
  • I'm sorry but I have to corridge myself: with this method you obtain just an aproximation of the good circle, and not a very good one!. Doubling the rope doesn't give you the simmetric of the arc. – user84976 Jun 30 '16 at 16:06
0

If you can measure tangent angles in the diagram the following could be of use in a scaled geometrical construction:

$$ R_{old}= \dfrac{r_2^2-r_1^2}{ 2(r_2 \sin \beta - r_1 \sin \alpha )}$$

Along perpendicular bisector of given points $(1,2)$ mark old center of circle $O$ with this radius and a new center $N$ with a new desired (increased/reduced) radius passing through $(1,2)$ on bisector. Sketch not to scale.

The above result for Irregular Pie is obtained by eliminating invariant semi-chord length $L$ from Circle property that product of two line segments is constant. $$ r\cdot (2 R \sin \theta -r)= L^2 $$

Patio Extension Plan

EDIT1

Yet another practical way to find $R$ is the relation $ R = \dfrac{s}{\alpha_ d +\beta_d} $ for Diagon from the Gauss-Bonnet theorem. Arc length $s=1P2 $ and corner angles are to be measured.

Narasimham
  • 42,260