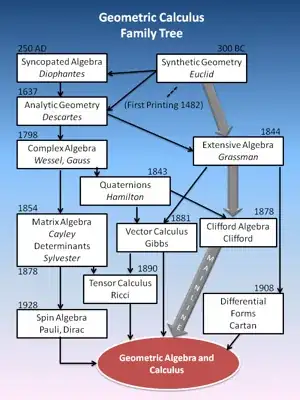
According to Wikipedia and some papers:
Exterior algebra = Grassmann algebra (= differential forms, since they are a construction of the exterior algebra) (=derivations, since derivations are just one possible construction of the dual object to differential forms).
EDIT: To make the claim that "exterior algebra=differential forms" precise, since as it stands it is not accurate/precisely formulated, make note of the fact that, as @user349357 points out, "the algebra of differential forms can also be viewed as an exterior algebra (taken over $C^{\infty}$) of the 1-forms".
Also, we can make note of the fact that for the geometric algebra (over $\mathbb{R}^n$) there is a natural embedding of the exterior algebra (over $\mathbb{R}^n$) inside of it, so we should expect that, by finding a suitable identification of 1-vectors and 1-forms, we should be able to identify the differential forms over $\mathbb{R}^n$ with an embedding inside of the geometric algebra over $\mathbb{R}^n$; David Hestenes has given a more comprehensive description of this process, to be found here. /EDIT
Multilinear algebra contains differential forms as a special case, so exterior=Grassmann algebra=outer/wedge product are contained in multilinear algebra.
Quadratic forms are just a special case of bilinear forms which are a special case of multilinear algebra.
Quadratic forms are also a special type of tensor, which is a special type of tensor algebra.
Both inner and outer products are special types of operations encompassed by geometric algebras.
Real numbers, complex numbers, quaternions, spinors, and rotors are all just objects in a real geometric algebra. Spinors are the even-grade subalgebra of geometric algebra I believe.
EDIT: Octonions are a non-associative algebra over the reals, whereas every Clifford algebra is an associative algebra by definition. Therefore octonions cannot be encompassed within either the geometric algebra or the more general Clifford algebra framework. Octonions are in fact the first non-associative real division algebras (with the associative real division algebras being the reals, the complex numbers, and the quaternions, all of which fit within the geometric algebra framework). /EDIT
A Clifford algebra is an algebra which relates a vector space over any type of a field to some type of quadratic form. (This is CLEARLY more general than whatever Clifford wrote about in the 19th century, which in my opinion is a complete misnomer which serves only to confuse the uninitiated.)
A geometric algebra is just a special type of Clifford algebra, any Clifford of a vector space over the real numbers.
Also apparently every multivector is a tensor, but not vice versa. See what's the relationship of tensor and multivector. These two documents (1) (2) give detailed explanations of how to represent some multivectors as tensors.
An exterior/Grassmann algebra is just a Clifford algebra using a degenerate quadratic form.
The quadratic form aspect aspect of Clifford algebras is probably then somehow be related to Riemannian metrics, and the choice of Euclidean vis a vis Minkowski/Lorentz metric determines what type of geometry is done.
In fact I think that Wikipedia implies that spacetime algebras are just a special type of geometric algebra contingent upon the correct choice of metric (the Minkowski/Lorentz metric), allowing us to use them for relativistic physics, while geometric algebra with the Euclidean metric allows us to describe classical physics.
The relationship to Riemannian metrics implicit in the quadratic forms which are part of geometric/Clifford algebras probably constitutes their connection to differential geometry, and probably means the latter has something to do with the Riemannian Clifford algebra also called the orthogonal Clifford algebra according to Wikipedia.
The representation of quadratic forms as square symmetric matrices also allows us to represent Riemannian metrics as square symmetric matrices.
A Clifford algebra is the quotient of a tensor algebra.
Also, since Clifford algebras are endowed with a quadratic form, which is a special case of a bilinear form, which is an object from multilinear algebra, and since vector spaces are described linear algebra which is a special case of multilinear algebra, and since Clifford algebras consist of a quadratic form and a vector space related somehow, they must also be a special case of multilinear algebra.
Dual objects exist in any linear or vector algebra framework, hence also in geometric algebras, which generalize linear algebra/vector spaces/vector calculus, and also in multilinear algebra, which also generalizes linear algebra.
Since matrices are part of linear algebra, then they must be a special case of multilinear algebra. Matrices also provide coordinate representations for rank 2 tensors, therefore must be special cases of tensor analysis, which itself is a special case of tensor algebra.
Pseudoscalars are just the dual objects to scalars, hence are special cases of exterior and geometric algebras, they are also equivalent to volume elements and hence determinants, and hence are a special case of multilinear algebra.
Bra-kets are just vectors and dual vectors and hence are generalized by geometric (hence Clifford and tensor) algebras as well as multilinear algebra.
I think covectors and pseudovectors are both just bras (the dual objects to vectors), although I am not entirely certain.
I have no idea how Lie algebras relate to the others. I know they are related to Lie groups, which are generalizations of matrix groups, which are special cases of both tensor and multilinear algebra as a result, but that is all I know. The generalization afforded by Lie algebras could be in an entirely different direction as far as I know.
EDIT: is does seem that the generalization is likely in a different direction, since Lie algebras provide many examples of non-associative algebras, whereas all Clifford algebras, and I believe even all tensor algebras, are associative by definition.
Also, as @user349357 points out, "any associative algebra gives a Lie algebra (in a functorial way) by taking commutators". So even if Lie algebras are not necessarily sub-algebras of the tensor/multilinear algebra, it still follows that they are natural objects of study for those algebras as much as commutators are natural objects of study./EDIT
What is the difference between tensor algebras and graded algebras? Is the former just the simplest case of the latter? Is multilinear algebra also a graded algebra?
Also what is the relationship between tensor algebras and multilinear algebra? (since these seem like the two most general objects to me based on the above).
EDIT: Multilinear algebra is a subject, not really an object, which studies tensors. A tensor algebra is a graded algebra consisting of all of the tensors of all orders which are generated from the underlying vector space. There are other types of graded algebras, saying an algebra is a graded algebra just means that it is a direct of subspaces indexed by the natural numbers, so is more of a descriptive term (adjective) than a name (noun). So confusingly enough, multilinear algebra is essentially the study of tensor algebras, because the word "tensor" is just a fancy way of saying "tensor product of vectors and/or dual/co-vectors" (in the simplest cases $n$-dimensional arrays), and multilinear maps/transformations are the structure-preserving functions which act on tensors, hence the name multilinear algebra. (For instance the determinant is just a multilinear map that takes $n$ vectors as an argument.) So the fact that geometric and Clifford algebras to generalize to both multilinear algebra and tensor algebras is not only not problematic and to be expected, it is essentially tautological. Thus the relationship between all of these structures is actually much cleaner/simpler to be expected than would be feared. /EDIT
If I want to understand "all of them", should I learn tensor analysis and tensor algebra or multilinear algebra? Is one a generalization of the other?
EDIT It seems like the best way to do this would be to learn about/understand tensor=multilinear algebra over an arbitrary commutative ring, understand how to consider the symmetric and exterior algebras over the same ring as both (1) quotients of that tensor algebra and (2) sub-algebras of that tensor algebra. Then learn/understand how the structures over $\mathbb{R}^n$ ("tensor analysis") can be considered special cases of this framework.
If outer products correspond to exterior algebras, then do inner products correspond to symmetric algebras?
EDIT: Yes, they do. At least for geometric algebras (which are a type of Clifford algebra over fields with characteristic zero), the symmetric tensors in the tensor algebra generated by the reals can be naturally identified with the elements of the symmetric algebra formed by quotienting the tensor algebra. The symmetric product has the form $$vw \mapsto \frac{1}{2} \left( v \otimes w + w \otimes v \right),$$ which is exactly the geometric inner product. Hence for a given associative tensor algebra, the corresponding Clifford algebra generalizes both its symmetric and exterior algebras. So the claim that Clifford algebras are more general than Grassmann algebras is clearly very true. /EDIT
Why do people claim that geometric algebra is all-encompassing when it is a special case of a Clifford algebra which is a special case of tensor algebra as well as a special case of multilinear algebra?
EDIT Usually when making such claims, people are only referring to other algebras over $\mathbb{R}^n$, of which the geometric algebra is a special case. Obviously it is not and could not be a generalization of arbitrary multilinear modules or Clifford modules over any commutative ring. When they say that it subsumes "everything" they are usually only referring to the use of exterior or symmetric algebraic structures over $\mathbb{R}^n$ (e.g. quaternions or spinors or cross products), and not all arbitrary tensors over $\mathbb{R}^n$ which it clearly does not subsume. In fact, while there definitely cannot exist an embedding of the tensor algebra over $\mathbb{R}^n$ into the geometric algebra over $\mathbb{R}^n$, an embedding in the opposite direction presumably could exist, although there may not exist any "natural" or "canonical" choice for such an embedding.
A simple way to phrase the above is that while geometric algebra over $\mathbb{R}^n$ may subsume vector algebra (over the same space), it does not subsume matrix algebra over the same space (although here we should be careful, because it does arguably subsume some special subclasses of matrices, for instance the use of orthogonal matrices to represent rotations). See this question for more details on this topic. /EDIT