1

Let $\mu(n)$ be the Möbius function and let $a(n)$ be the Dirichlet inverse of the Euler totient function:

$$a(n) = \sum\limits_{d|n} d \cdot \mu(d)$$

Let the matrix $T$ be defined as:

$$T(n,k)=a(GCD(n,k))$$

where GCD = the Greatest Common Divisor.

This matrix $T$ starts:

$$T = \left( \begin{array}{ccccccc} +1&+1&+1&+1&+1&+1&+1&\cdots \\ +1&-1&+1&-1&+1&-1&+1 \\ +1&+1&-2&+1&+1&-2&+1 \\ +1&-1&+1&-1&+1&-1&+1 \\ +1&+1&+1&+1&-4&+1&+1 \\ +1&-1&-2&-1&+1&+2&+1 \\ +1&+1&+1&+1&+1&+1&-6 \\ \vdots&&&&&&&\ddots \end{array} \right)$$

There is then the symmetry that the von Mangoldt function can be computed as: $$\Lambda(n) = \sum\limits_{k=1}^{k=\infty}\frac{T(n,k)}{k}$$

$$\Lambda(k) = \sum\limits_{n=1}^{n=\infty}\frac{T(n,k)}{n}$$

In the language of Dirichlet series this is equivalent to: $$\Lambda(n)=\lim\limits_{s \rightarrow 1} \zeta(s)\sum\limits_{d|n} \frac{\mu(d)}{d^{(s-1)}}$$

Can we then say that the Dirichlet series generating function for the whole matrix $T$ is:
$$\sum\limits_{k=1}^{\infty}\sum\limits_{n=1}^{\infty} \frac{T(n,k)}{n^c \cdot k^z} = \sum\limits_{n=1}^{\infty} \frac{\lim\limits_{s \rightarrow z} \zeta(s)\sum\limits_{d|n} \frac{\mu(d)}{d^{(s-1)}}}{n^c} = \frac{\zeta(z) \cdot \zeta(c)}{\zeta(c + z - 1)}$$?

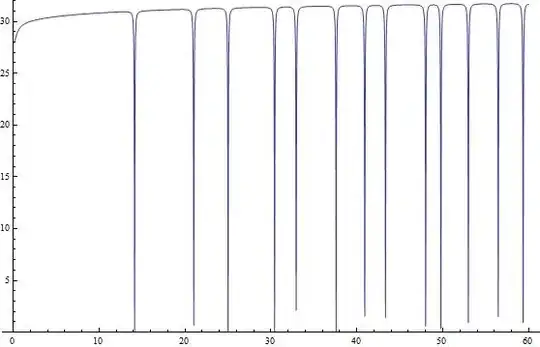
For $c$ a value close to one such as $c=1+\frac{1}{30}$ we have this plot for $\frac{\zeta (c) \zeta (\frac{1}{2}+i t)}{\zeta (c+\frac{1}{2}+i t-1)}$ on the critical line in the complex plane:

Dirichlet series spectra

where the downward spikes are at Riemann zeta zeros.

(*Mathematica 8 start*)
Clear[s, z, c]
z = 9
c = 7
N[Zeta[z]*Zeta[c]/Zeta[c + z - 1], 20]
N[Sum[Limit[
    Zeta[s] Total[1/Divisors[n]^(s - 1)*MoebiusMu[Divisors[n]]], 
    s -> z]/n^c, {n, 1, 64}], 20]
Clear[c, ss, t]
ss = 30
c = 1 + 1/ss;
sigma = 1/2;
Plot[Re[N[Zeta[sigma + I*t]*Zeta[c]/Zeta[c + sigma + I*t - 1], 
   20]], {t, 0, 60}, PlotRange -> {0, ss + 2}]
(*Mathematica 8 end*)
Community
  • 1
Mats Granvik
  • 7,614
  • 1
    I think you should look at $\sum_{k \ge 1} k^{-s} T(n,k) = \sum_{k \ge 1} k^{-s} \sum_{d | gcd(n,k)} \mu(d) d = \sum_{d | n} \mu(d) d \sum_{k \ge 1, d | k} k^{-s} = \sum_{d | n} \mu(d) d \sum_{m \ge 1} (md)^{-s} = \sum_{d | n} \mu(d) d^{1-s} \zeta(s) $ – reuns Jun 19 '16 at 17:22
  • 1
    so that $$\sum_k \sum_n n^{-z} k^{-c} T(n,k) = \zeta(c) \sum_n n^{-z} \sum_{d | n} \mu(d) d^{1-c} $$ on the other hand $$\frac{\zeta(z)}{\zeta(z+c-1)} = \sum_n n^{-z} \sum_k \mu(k) k^{-z-c+1} =\sum_m m^{-z} \sum_{d | m} \mu(d) d^{1-c}$$ – reuns Jun 19 '16 at 17:28
  • Mathematica tells me:

    $$-\frac{\zeta '(s)}{\zeta (s)}=\lim_{c\to 1} , \left(\frac{\zeta (c) \zeta (s)}{\zeta (c+s-1)}-\zeta (c)\right)$$

     – Mats Granvik Jun 26 '16 at 14:25
  • 1
    mathematica told me... as $c \to 1$ : $\zeta(c) = \frac{1}{c-1}+ \mathcal{O}(1)$ and with $f(c) = \frac{1}{\zeta(c+s-1)}$, $\ f(c) =f(1)+(c-1)f'(1) + o(c-1)$ where $f(1) = \frac{1}{\zeta(s)}$ and $f'(1) = -\frac{\zeta'(s)}{\zeta(s)^2}$ hence $$\lim_{c \to 1} \zeta(c) \left(\frac{\zeta(s)}{\zeta(c+s-1)}-1\right) =\lim_{c \to 1} (\frac{1}{c-1}+\mathcal{O}(1))\left(\zeta(s)(f(1)+(c-1)f'(1) + o(c-1))-1\right) $$ $$= \lim_{c \to 1} (\frac{1}{c-1}+ \mathcal{O}(1))\left(-(c-1)\frac{\zeta'(s)}{\zeta(s)}+ o(c-1)\right) = \ldots$$ – reuns Jun 26 '16 at 18:52

1 Answers1

0

joriki proved here that for $n>1$ the von Mangoldt function is:

$$\Lambda(n)=\displaystyle \sum\limits_{k=1}^{\infty}\frac{T(n,k)}{k}$$

so if $$\frac{\zeta (c) \zeta (s)}{\zeta (c+s-1)}$$ is to be the generating function associated with the double sum:

$$\sum\limits_{k=1}^{\infty}\sum\limits_{n=1}^{\infty} \frac{T(n,k)}{n^c \cdot k^s} = \frac{\zeta(s) \cdot \zeta(c)}{\zeta(c + s - 1)}$$

(explicitly valid for $c>1$ and $s>1$), then when subtracting $\zeta(c)$, which is the first column in the matrix $T$, we should get the Dirichlet generating function for the von Mangoldt function $\Lambda(n)$:

$$\sum _{n=1}^{\infty } \frac{\Lambda (n)}{n^s}=-\frac{\zeta '(s)}{\zeta (s)}=\lim_{c\to 1} \, \left(\frac{\zeta (c) \zeta (s)}{\zeta (c+s-1)}-\zeta (c)\right)$$

which we do according to Mathematica.

Community
  • 1
Mats Granvik
  • 7,614
  • as $c \to 1$ : $\zeta(c) = \frac{1}{c-1}+\gamma+\mathcal{O}(c-1)$. Do you get that (this is the Taylor expansion of the analytic function $\zeta(c) (c-1)$) ? And again from the Taylor expansion $\zeta(s+c-1)= \zeta(s)+ (c-1)\zeta'(s)+\mathcal{O}((c-1)^2)$ so that $$\lim_{c \to 1}\frac{\zeta(c)\zeta(s)}{\zeta(c+s-1)}-\zeta(c) = \lim_{c \to 1}\frac{1}{c-1}(\frac{\zeta(s)}{\zeta(s)+(c-1)\zeta'(s)+\mathcal{O}((c-1)^2)}-1)=\lim_{c \to 1}\frac{1}{c-1}\frac{-(c-1)\zeta'(s)}{\zeta(s)+(c-1)\zeta'(s)}=\frac{-\zeta'(s)}{\zeta(s)}$$ – reuns Nov 28 '16 at 01:54
  • This is detailed in any real analysis course – reuns Nov 28 '16 at 01:54