7

Suppose we want to solve following optimization problem (it is a PCA problem in this post)

$$ \underset{\mathbf w}{\text{maximize}}~~ \mathbf w^\top \mathbf{Cw} \\ \text{s.t.}~~~~~~ \mathbf w^\top \mathbf w=1 $$

As mentioned the the post, using the Lagrange multiplier, we can change the problem into

$$ {\text{minimize}} ~~ \mathbf w^\top \mathbf{Cw}-\lambda(\mathbf w^\top \mathbf w-1) $$ Differentiating, we obtain $\mathbf{Cw}-\lambda\mathbf w=0$, which is the eigenvector equation. Problem solved and $\lambda$ is the largest eigenvalue.

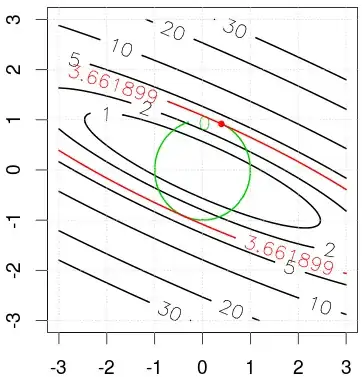
I am trying to do a numerical example here to understand more about how Lagrange multiplier changed the problem, but getting inconsistent results (the following figure shows geometric solution to the problem, but in order to get the same results, I need to change the sign on $\lambda$ in my code.).

enter image description here

X=iris[,c(1,3)]
X$Sepal.Length=X$Sepal.Length-mean(X$Sepal.Length)
X$Petal.Length=X$Petal.Length-mean(X$Petal.Length)
C=cov(X)
r=eigen(C)

obj_fun<-function(x){
  w=as.matrix(c(x[1],x[2]),ncol=1)
  lambda=r$values[1]
  v=t(w) %% C %% w + lambda (t(w) %% w -1)
  return(as.numeric(v))
}


gr<-function(w) {
  lambda=r$values[1]
  v=2* C %% w + 2lambda* w
  return(v)
}


library(optimx)
res=optimx(c(1,2), obj_fun,gr, method="BFGS")`

enter image description here

Could anyone tell me if I am correct in code? and the sign before $\lambda$ should be a positive or negative.

Also sorry about R code in math community, I was trying to ask it in statistics community but got no answer. All the code is about to write down a minimization problem and replace $\lambda$ with the largest eigenvalue. Then solve it using library.

Rodrigo de Azevedo
  • 23,223
hxd1011
  • 493

1 Answers1

1

I think I got the answer by myself but wish some experts can confirm.

The confusion is that, in CVX book we are converting one optimization problem with constraints to another optimization problem without constraints and solve the dual problem. But in PCA optimization we cannot.

For example, page 227, we convert

$$ \underset{x}{\text{minimize}}~~ x^\top x \\ \text{s.t.}~~~~~~ Ax=b $$

into maximize the dual function $g(v)$

$$ \underset{x}{\text{maximize}}~~g(v)~~= \underset{x}{\text{maximize}}~~-(1/4)v^\top A A^\top v -b^\top v \\ $$

In PCA optimization problem, problem has Lagrangian (for equality constraint we can use $-\lambda$)

$$ \mathcal{L}(\mathbf w,\lambda)=\mathbf w^\top \mathbf{Cw}-\lambda(\mathbf w^\top \mathbf w-1) $$

For fixed $\lambda$, we get partial derivative and set to $\mathbf 0$.

$$ \frac{\partial \mathcal{L}}{\partial \mathbf w}=\mathbf 0=2\mathbf {Cw}-2\lambda\mathbf w $$

which is the eigenvector equation

$$ \mathbf {Cw}=\lambda\mathbf w $$

As pointed out by Matthew Gunn in the comment, PCA problem the objective is not convex see this discussion. Therefore we should not try to minimize dual function to solve the original problem.

Instead we should solve the eigen vector equation and we should not use R to verify the solution by minimize dual function $g(\lambda)$.

hxd1011
  • 493