12

This question spawned from a recent, very interesting problem.

Let $\varphi=\frac{1+\sqrt{5}}{2}$ and $T$ denote the map on the space of continuous probability density functions supported over $\left(0,\varphi\right)$, defined by $$ (T f)(x) = 2x\cdot\left( f * \mathbb{1}_{(0,1)}\right)(x^2). \tag{1}$$ What are the fixed points of $T$?

If we assume that $T(f_n)=f_{n+1}$ and that $f_n$ is the PDF of $X_n$, we are simply looking for the limit distribution of the Markov chain $(X_n)$ defined by

$$X_{n+1}=\sqrt{U_{n+1}+X_n},$$

where $(U_n)_{n\geqslant1}$ is i.i.d. uniform on $(0,1)$ and independent of $X_0$. One might be tempted to switch to Fourier transforms/series in (1), but the $x^2$ term does not make this approach very attractive.

In the comments to the original question, user Did proved that, assuming $f_1(x)=2x\cdot\mathbb{1}_{(0,1)}$, i.e. $X_0=0$, we have $\mathbb{E}[X_n]< \frac{1+\sqrt{3}}{2}$ for every $n\geqslant1$, by convexity. Numerical simulations suggest that $\lim\limits_{n\to +\infty}\mathbb{E}[X_n]$ is very close to $\frac{1+\sqrt{3}}{2}$, but the exact value of the limit depends on the answer to this question.

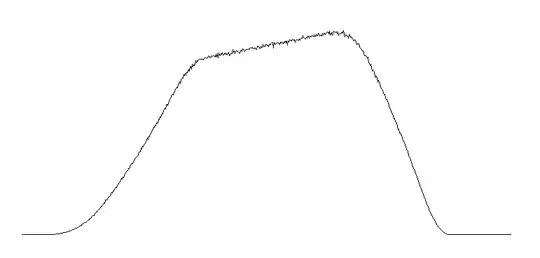
Thanks to mercio, here it is how the limit distribution looks like, over the interval $[1,\varphi]$:

enter image description here

Community
  • 1
Jack D'Aurizio
  • 361,689
  • $f_1$ is obtained from a dirac delta distribution (at $0$) as $f_0$. Also I think a fixed point $f$ necessarily has $f=0$ on $[0;1]$. – mercio Jun 13 '16 at 13:52
  • if you let $X_0 = 1$ and $X_{n+1} = \sqrt{X_n + U_{n+1}}$ and plot the first few million values in a histogram chart you should obtain something like a graph of $f$. We can see its affine part ($f(x) = 2x$ for $x \in [\sqrt \varphi ; \sqrt 2]$) – mercio Jun 13 '16 at 14:30
  • @mercio: if you already plotted it, could you post your mentioned histogram? – Jack D'Aurizio Jun 14 '16 at 13:18
  • 2
    plotting 10 million values gives this http://imgur.com/xzu2kDS (the x coordinate goes from $1$ to $1.7$) – mercio Jun 15 '16 at 13:45
  • 2
    A quick observation: Since $\phi \geq X_n \geq \max{U_1, \cdots, U_n}$, the limiting distribution should be supported on $[1, \phi]$. – Sangchul Lee Jul 22 '16 at 19:21

0 Answers0