4

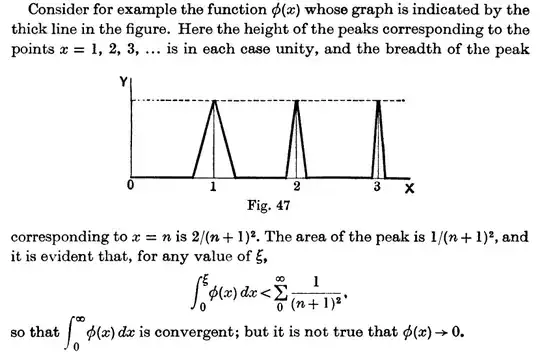
Let $f:\Bbb R\to \Bbb R$ be a continuous function such that $\int _0^\infty f(x)\text{dx}$ exists.

Prove that

  • If $\lim _{x\to \infty } f(x)$ exists, then $\lim_{x\to \infty} f(x)=0$

  • If $f$ is non-negative then $\lim _{x\to \infty } f(x)$ must exist and $\lim_{x\to \infty} f(x)=0$

My try

To prove that $\lim_{x\to \infty} f(x)=0$ we should show that $\exists G>0$ such that $x>G\implies |f(x)|<\epsilon $ for any $\epsilon>0$

But I can't find out how to show this. Please help.

Soumik Mukherjee
  • 746
  • 1
  • 5
  • 15
Learnmore
  • 31,675
  • 10
  • 110
  • 250

2 Answers2

3

This is pretty standard. Let $F(x) = \int_{0}^{x}f(t)\,dt$ then we are given that $\lim_{x \to \infty}F(x) = L$ exists. Now by continuity of $f$ and fundamental theorem of calculus we have $F'(x) = f(x)$ and we are given that $\lim_{x \to \infty}f(x) = \lim_{x \to \infty}F'(x) = M$ also exists. We can see via mean value theorem that $$F(x + 1) - F(x) = F'(\xi) = f(\xi)$$ where $x < \xi < x + 1$. Letting $x \to \infty$ in the above equation and noting that $\xi \to \infty$ we get $$L - L = M$$ or $M = 0$ so that $f(x) \to 0$ as $x \to \infty$.

Second statement is false and counterexample is in the following figure (taken from the masterpiece A Course of Pure Mathematics by G. H. Hardy):

enter image description here

Paramanand Singh
  • 92,128
-2

For all $n\in \mathbb{N}$ larger than 1,

Let $$ f(x)= \begin{cases} 0 \ for \ x\leq n \\ n^4x-n^5 \ for \ n<x\leq n+1/n^3 \\ -n^4+2n+n^5 \ for \ n+1/n^3<x\leq n+2/n^3 \end{cases}$$ By some calculation $\int_n^{n+1}f(x)dx=1/n^2$. Then $\int_0^\infty f(x) = \sum_{n=2}^\infty 1/n^2$.

But $lim_{x \to \infty} f(x)$ does not exist.

Seongqjini
  • 1,261