Nature and number of solutions to $xy=x+y$

Question

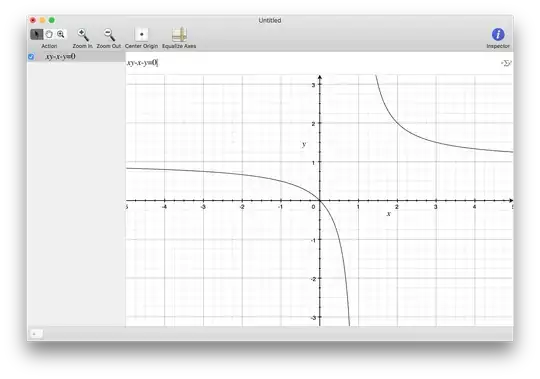
Find all solutions to $$xy=x+y$$ Initially the given condition was $x,y\in \Bbb{Z}$.

$$$$In this case, I just guessed that the solutions were $(0,0)$ and $(2,2)$. As far as I can see, these are the only 2 integral solutions possible. However, i'm quite surprised as usually a Diophantine Equation has infinite solutions. Could somebody please show me how to actually $solve$ this equation instead of just guessing the values? Is there any way to $show$ that there are just 2 sets of solutions?

$$$$Secondly, what if $x,y\in \Bbb{R}$? In that case how could the equation be solved? $$$$For both these conditions on the values of $x,y$, is there any way to use Coordinate Geometry to achieve an answer? $$$$ Many thanks in anticipation!

Edit: I forgot to mention that I know the solution using factoring. I was hoping to find a solution using Coordinate Geometry. I was told by a friend that the non integral solutions lie on 2 unique lines, and am hence particularly interested in a geometrical solution.

Answer 1

Of course the simplest solution is to write the equation as $(x-1)(y-1)=1$.

---

The curve $xy-x-y=0$ is a hyperbola with asymptotes $x=1$ and $y=1$.

Its graph is so contained in the union of the strips

$$ (-\infty,0]\times[0,1), \qquad [0,1)\times(-\infty,0], \qquad (1,2]\times[2,\infty), \qquad [2,\infty)\times(1,2] $$

The only points with both integer coordinates are $(0,0)$ and $(2,2)$.

More analytically, consider the curve written as $$ y=1+\frac{1}{x-1}=\frac{-x}{1-x} $$ If $x>2$, then $x-1>1$, so $1<y<2$, so $y$ is not integer. If $x<0$, then $0<y<1$, so $y$ is not integer. For $0<x<1$ and $1<x<2$, $x$ is not integer.

Thus only $x=0$ or $x=2$ remain.

Answer 2

You can say: $x = u+v\\ y = u-v\\$

plug it into your equation and you get:

$u^2 - v^2 = 2u\\ (u-1)^2 - v^2 = 1$

And you should recognize that as a hyperbola. And have a idea how to get solutions in terms of $(u,v)$. And then use the substitution again to get those solutions in terms of $(x,y)$.

What have I done? I have changed the coordinate system such that the line $y=x$ is my new "$u-$axis" and $y = -x$ is my new "$v-$axis." That is, I have rotated the system 45 degrees.

Now someone is going to give me grief (unless I am able to dispel it....) The change that I made does not preserve distance. So, everything is a little bit compressed in the new coordinate system.

To which I say, is that such a big deal?

If I were a good boy, I would have said:

$u = x \cos \frac\pi4 - y\sin \frac\pi4 \\ v = x \sin \frac\pi4 + y\cos \frac\pi4 $

$x = \frac {\sqrt 2}{2} (u+v)\\ y = \frac {\sqrt 2}{2} (v-u)$

Swapping my u's and v's.

$v^2 - u^2 = 2\sqrt 2 v\\ (v- \sqrt 2)^2 - u^2 = 2$

Giving a very similar equation.

Answer 3

To solve $x+y=xy$ in integers, note that it implies that $x\mid y$ and $y\mid x$. Therefore, $y=\pm x$. Can you show from there that $(0,0)$ and $(2,2)$ are the only integer solutions?

Answer 4

Clearly, $a\ne1.$ Solving for $b$: $$b={a\over a-1}\tag1$$ If $a=0.$ then (1) gives the solution $(a.b)=(0,0).$ Otherwise, the numerator and denominator in (1) are coprime, implying that $a=1\pm1,$ giving exactly one more solution, namely $(2,2).$

Answer 5

In the case that$(x,y) \in \Bbb{Q}$, setting $x=\frac{2}{1-u}$ and $y=\frac{2}{1+u}$ then

$x+y=\frac{4}{1-u^{2}}$

$x y=\frac{4}{1-u^{2}}$

and

if $ 0<u<1$ then $ (x,y)>(0,0)$.

If $u=\frac{1}{2}$ then $ (x,y)>(4, 4/3)$ and so on…