Parametric equations for intersection between plane and circle

Question

So I was looking at this question Determine Circle of Intersection of Plane and Sphere but I need to know how to find a parametric equation for intersections such as these. My particular question is to find a parametric equation for the intersection between the plane

$$x+y+z=1$$ and unit sphere centered at the origin.

I started out my question by substituting $$ z=-x-y+1$$ into $$x^2+y^2+z^2=1 $$ deriving $$x^2+y^2+(-x-y+1)^2=1$$ and getting $$2x^2+2y^2+2xy-2x-2y=0$$ but I am unsure how to proceed from here.
I also tried to use the vector equation of the plane $$r(u, v)=(0,0,1)+(2,1,-3)u+(1,1,-2)v$$ but I am not sure how that would help.

Answer 1

Steven Gregory gives an excellently crafted solution.

One can also approach the problem from the standpoint of a particle moving at a constant velocity in a circle through the points $(1,0,0),\,(0,1,0),\,(0,0,1)$ centered at $\left(\tfrac{1}{3},\tfrac{1}{3},\tfrac{1}{3}\right)$. The radius of this circle is $\sqrt{\tfrac{2}{3}}$.

This suggests using a sinusoidal for each coordinate with phase shifts adjusted "equally around the circle" so to speak. Something like

\begin{equation} x(t)=\tfrac{1}{3}+\sqrt{\tfrac{2}{3}}\cos(t) \end{equation} \begin{equation} y(t)=\tfrac{1}{3}+\sqrt{\tfrac{2}{3}}\cos\left(t+\tfrac{2\pi}{3}\right) \end{equation} \begin{equation} z(t)=\tfrac{1}{3}+\sqrt{\tfrac{2}{3}}\cos\left(t-\tfrac{2\pi}{3}\right) \end{equation}

A check confirms that

\begin{equation} x(t)+y(t)+z(t)=1 \end{equation}

and

\begin{equation} x^2(t)+y^2(t)+z^2(t)=1 \end{equation}

Answer 2

The plane $ \zeta = \{(x,y,z) : x + y + z = 1\},$ is perpendicular to the vector $\langle 1,1,1 \rangle$.

Two points on $\zeta$ are $\mathbf O = \left( \dfrac 13,\ \dfrac 13,\ \dfrac 13 \right) \text{ and } \mathbf A = (0,0,1)$.

Since $\overrightarrow{\mathbf{OA}} = \dfrac 13 \langle -1, -1, 2 \rangle$, the unit vector $\overrightarrow u = \dfrac {1}{\sqrt 6} \langle -1, -1, 2 \rangle$ is parallel to the plane $\zeta$.

Since $\overrightarrow{\mathbf{OA}} \times \langle 1,1,1 \rangle = \langle -1, 1, 0 \rangle$, then the unit vector $\overrightarrow v = \dfrac{1}{\sqrt 2} \langle -1, 1, 0 \rangle$ is parallel to the plane $\zeta$ and $\overrightarrow u \perp \overrightarrow v$.

So we can parameterize the plane, $\zeta$ as $$\zeta(s,t) = \mathbf O + s \overrightarrow u + t \overrightarrow v = \left( \dfrac 13 - \dfrac{s}{\sqrt 6} - \dfrac{t}{\sqrt 2}, \dfrac 13 - \dfrac{s}{\sqrt 6} + \dfrac{t}{\sqrt 2}, \dfrac 13 + \dfrac{2s}{\sqrt 6} \right)$$

As ugly as the following looks

$$\left( \dfrac 13 - \dfrac{s}{\sqrt 6} - \dfrac{t}{\sqrt 2}\right)^2 + \left( \dfrac 13 - \dfrac{s}{\sqrt 6} + \dfrac{t}{\sqrt 2}\right)^2 + \left( \dfrac 13 + \dfrac{2s}{\sqrt 6}\right)^2 = 1 $$

It simplifies to $s^2 + t^2 = \dfrac 23$

So we let $s = \sqrt{\dfrac 23}\cos \theta$ and $t = \sqrt{\dfrac 23}\sin \theta$ and simplify. We get

$$\zeta(s,t) = \left( \dfrac 13 - \dfrac {\cos \theta}{3} - \dfrac{\sin \theta}{\sqrt 3},\; \dfrac 13 - \dfrac {\cos \theta}{3} + \dfrac{\sin \theta}{\sqrt 3},\; \dfrac 13 + \dfrac {2\cos \theta}{3} \right)$$

a more intuitive answer

---

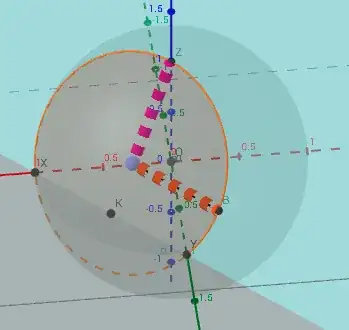
Let $S$ be the unit sphere $x^2 + y^2 + z^2 = 1$.

Let $P$ be the plane $x + y + z = 1$.

Let $C$ be the circle $C = S \cap P$.

The unit vector $U = \dfrac{1}{\sqrt 3} \langle 1,1,1 \rangle$ is perpendicular to $P$.

The line $x = y = z$

• passes through, $(0,0,0)$, the center of $S$

• passes through, $X$, the center of $C$

• is perpendicular to $P$

The distance from $P$ to the center of $S$ is $ \dfrac{\left| 0 + 0 + 0 - 1 \right|}{\sqrt{1^2 + 1^2 + 1^2}} = \dfrac{1}{\sqrt 3}$.

The center of $C$ is at $X = (0,0,0) + \dfrac{1}{\sqrt 3}U = \left( \dfrac 13,\dfrac 13, \dfrac 13 \right)$.

The radius of $C$ is $r = \sqrt{1 - \dfrac 13} = \sqrt{\dfrac 23}$.

We need to find two points, $A$ and $B$, on $C$ such that $\overrightarrow{XA} \perp \overrightarrow{XB}$.

• $A = (1,0,0)$ is a point on $C$.

• $\left \| \overrightarrow{XA} \right \| = \left \| \left( \dfrac 23, -\dfrac 13, -\dfrac 13 \right) \right \| = \sqrt{\dfrac 23}$

• $U \times \sqrt{\dfrac 32} \; \overrightarrow{XA} = \left( 0, \dfrac{1}{\sqrt 2}, -\dfrac{1}{\sqrt 2} \right)$ is a unit vector, in P, that is perpendicular to $\overrightarrow{XA}$.

• $\overrightarrow{XB} = \sqrt{\dfrac 23} \left( 0, \dfrac{1}{\sqrt 2}, -\dfrac{1}{\sqrt 2} \right) = \left( 0, \dfrac{1}{\sqrt 3}, -\dfrac{1}{\sqrt 3} \right)$

\begin{align} C &= X + \cos \theta \; \overrightarrow{XA} + \sin \theta \; \overrightarrow{XB} \\ C &= \left( \dfrac 13,\dfrac 13, \dfrac 13 \right) + \cos \theta \; \left( \dfrac 23, -\dfrac 13, -\dfrac 13 \right) + \sin \theta \; \left( 0, \dfrac{\sqrt 3}{3}, -\dfrac{\sqrt 3}{3} \right) \\ C &= \dfrac 13(1 + 2 \cos \theta, \; 1 - \cos \theta + \sqrt 3 \sin \theta, \; 1 - \cos \theta - \sqrt 3 \sin \theta) \end{align}

Answer 3

You can divide your equation by 2:

$$x^2+y^2+xy-x-y = 0$$ Let us toss the left hand side coefficients into a matrix: $$\left[\begin{array}{rrr}0&-1&1\\-1&1&0\\1&0&0\end{array}\right]$$

Now you can notice a symmetry. If treated as a matrix, it is symmetric. This makes reasonable the substitution $$\cases{x=s-t\\ y=s+t}$$ if we do it, we get (for the left hand side):

$$(s-t)^2+(s+t)^2+(s-t)(s+t) - (s+t)-(s-t)=\\ \underset{square 1}{\underbrace {s^2-2st+t^2}} +\underset{square 2}{\underbrace {s^2+2st+t^2}} + \underset{conjugate}{\underbrace {s^2-t^2}}-2s=\\ 3s^2+t^2-2s$$

Now this should be easier to work with and/or interpret.

Answer 4

First, let's name some points. Let $O=(0,0,0)$, $X=(1,0,0)$, $Y=(0,1,0)$, and $Z=(0,0,1)$. Let $A$ be the center of the circle we are trying to find. Let $K$ be the midpoint of $XY$. Note that $K=\left(\frac{1}{2},\frac{1}{2},0\right)$.

Let's consider right triangle $ZOK$:

We note that A is the base of the altitude to the hypotenuse. Since $OZ=1$ and $OK=\frac{\sqrt{2}}{2}$, $OA=\frac{\sqrt{3}}{3}$. Because $A$ must be of the form $(n,n,n)$, we conclude that $A=\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$. We can also calculate that $AZ=\frac{\sqrt{6}}{3}$. Note that $AZ$ is the radius of the circle.

Now, let's invent a new 2D coordinate system with new unit vectors. $A$ will be the center of this coordinate system. Rotate $AZ$ 90 degrees clockwise on the plane $x+y+z=1$. This new vector (orange) will be one of our unit vectors, which we will call $u$. The other will be $AZ$ itself (pink), which we will call $v$. Imagine extending vector $u$ into a line and moving it down to the $xy$-plane. It makes a 45-45-90 triangle with the $x$ and $y$ axes. Since $u$ has no $z$-component, we conclude that $u=\left(-\frac{\sqrt{6}}{3}\cdot\frac{\sqrt{2}}{2},\frac{\sqrt{6}}{3}\cdot\frac{\sqrt{2}}{2},0\right)=\left(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},0\right)$.

Drop a perpendicular from point A to the $z$ axis. Call the foot of this perpendicular $H$. Note that triangle $ZOA$ is similar to $ZOK$. Using this fact, we can calculate that $ZH=\frac{2}{3}$. Note that $ZH$ is the $z$-component of $v$. We can also calculate that $AH=\frac{\sqrt{2}}{3}$. Imagine moving $AH$ down to the $xy$-plane. We see that $AH$ forms 45 degrees with the $x$ and $y$ axes. We conclude that $v=\left(-\frac{\sqrt{2}}{3}\cdot\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{3}\cdot\frac{\sqrt{2}}{2},\frac{2}{3}\right)=\left(-\frac{1}{3},-\frac{1}{3},\frac{2}{3}\right)$.

The equation of the circle is $$A+u\cos(t)+v\sin(t)=\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)+\cos(t)\left(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},0\right)+\sin(t)\left(-\frac{1}{3},-\frac{1}{3},\frac{2}{3}\right)$$

Adding everything together, we get a final answer:

$$\frac{1}{3}\left(1-\sqrt{3}\cdot\cos(t)-\sin(t),1+\sqrt{3}\cdot\cos(t)-\sin(t),1+2\sin(t)\right)$$