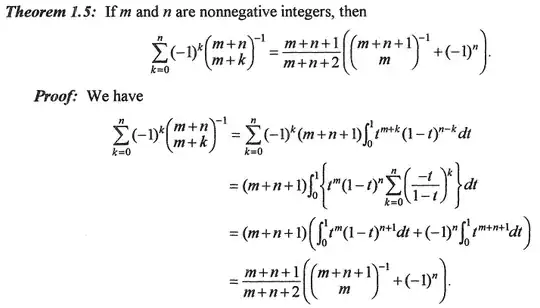If $n$ is an even natural number, then find $$\sum_{r=0}^n \left(\frac{(-1)^r}{\binom{n}{r}}\right)$$
I tried to solve the question using conventional method, by trying to use calculus, but I don't think that would be applicable here, because no binomial expansion (as far I as know) can give a coefficient in denominator hence I got stuck at it.
Just to give a self-contained proof through the Euler beta function:
$$\begin{eqnarray*}\sum_{r=0}^{n}(-1)^r\binom{n}{r}^{-1}&=&(n+1) \int_{0}^{1}\sum_{r=0}^{n}(-1)^r x^r (1-x)^{n-r}\,dx\\[0.2cm]&=&(n+1)\int_{0}^{1}(1-x)^n\sum_{r=0}^{n}\left(\frac{x}{x-1}\right)^r\,dx\\[0.2cm]&=&(n+1)\int_{0}^{1}(1-x)^n\frac{\left(\frac{x}{x-1}\right)^{n+1}-1}{\frac{x}{x-1}-1}\,dx\\[0.2cm]&=&(-1)^n (n+1)\int_{0}^{1}\left(x^{n+1}-(x-1)^{n+1}\right)\,dx\\[0.2cm]&=&(-1)^n (n+1)\left[\frac{1}{n+2}-\frac{(-1)^{n+1}}{n+2}\right]\\[0.2cm]&=&\color{red}{(1+(-1)^n)\cdot\frac{n+1}{n+2}}\end{eqnarray*}$$ but the same conclusion also follows from: $$ \binom{n}{r}^{-1} = \left(\frac{n+1}{r+1}-1\right)\binom{n}{r+1}^{-1} $$ plus induction.
Using the beta function, Trif gives a proof in his paper
COMBINATORIAL SUMS AND SERIES INVOLVING INVERSES OF BINOMIAL COEFFICIENTS
to a slightly more general statement:
You question corresponds to the case when $m=0$.
See also the paper Alternating Sums of the Reciprocals of Binomial Coefficients for a more general discussion about the sum $$ T_n^{(l,m)}=\sum_{k=0}^n(-1)^kk^l\binom{m+n}{m+k}^{-1}. $$