How can I construct a $2^{63}$-gon with a straightedge and compass?

Question

I entered $2^{63}$ as a stand alone value at WolframAlpha. Among the responses was a factoid that 'A regular 9223372036854775808-gon is constructible with a straightedge and compass.'

What is such a shape and how can I construct one?

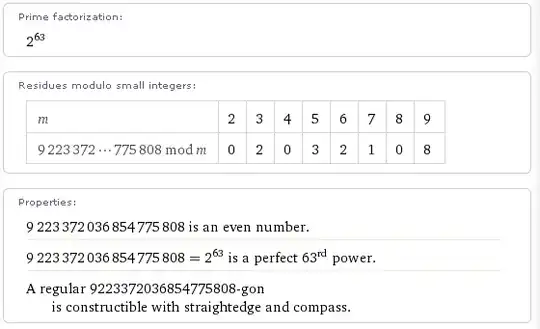
2^63-gon notice

And that is possible to repeat 62 times with a straightedge and paper? Isn't that akin to halving a sheet of paper and halving it again etc.? — zundarz, Aug 03 '12 at 20:28
You should probably try it with a heptagon first, before moving on to the hard stuff. — SiliconCelery, Aug 03 '12 at 20:52
See also: Can a circle's circumference be divided into arbitrary number of equal parts using straight edge and compass only? — t.b., Aug 03 '12 at 21:15
This is doable if you have a big enough piece of paper. At 1 inch per side, it'll only take a sheet 7.9 light years wide. Of course, the time to do the construction would be a bit daunting. — Rick Decker, Aug 03 '12 at 21:27

Ross Millikan · Accepted Answer · 2012-08-03T20:32:57.380

16

Start with a circle and a diameter. Bisect the diameter and extend the bisector to the circle to make a square. Bisect each right angle at the center of the circle $61$ times, extending the bisector to the circle. You have $2^{63}$ points, equally spaced, around the circle. As Dario says, you won't be able to tell it from the original circle.

The regular polygons constructible with straightedge and compass have the number of sides of the form $2^n$ times a product of zero or more of the Fermat primes: $3, 5, 17, 257, 65537$ (each to only the first power)

edited Aug 03 '12 at 20:32

answered Aug 03 '12 at 20:26

Ross Millikan

383,099

This will probably be indistinguishable from the way that I usually draw regular $2^{63}$-gons: place the point of the compass and draw a circle. – robjohn Aug 03 '12 at 20:42
I strongly doubt that you'll have $2^{63}$ equally spaced points after this procedure. Even if you just make an error of only 0.1% per step, you'll have a total error of more than 6% in the last constructed points. – celtschk Aug 03 '12 at 20:48
3

@PeterTamaroff: speak for yourself. – robjohn Aug 03 '12 at 20:50
@robjohn Fair enough. – Pedro Aug 03 '12 at 20:51
@PeterTamaroff: But an idealist will also be able to distinguish between a circle and a $2^{63}$-gon. – celtschk Aug 03 '12 at 20:51
@celtschk Maybe some nanometrics should be involved here? You're right. – Pedro Aug 03 '12 at 20:52
A few beers and a mighty fine compass would improve my accuracy too. – zundarz Aug 03 '12 at 20:54
4

@celtschk: my errors are random, so they only build up as $\sqrt n$, making about $0.8%$ at the end. As $2^{63} \approx 9.2\cdot 10^{18}$ this would be $7.4$ parts in $10^{20}$ of the original circle diameter. I challenge you to find it. – Ross Millikan Aug 03 '12 at 21:41

How can I construct a $2^{63}$-gon with a straightedge and compass?

1 Answers1