How to prove this geometry inequality (1) with $2(DF+EF)\ge BC$

Question

There is a picture which hope to illustrate the configuration:

$\triangle ABC$ is such that $\angle A=\dfrac{2\pi}{3}$, and $F$ is the midpoint of $BC$, and $D,E$ lie on $AB,AC$ respectively, such that $DE ||BC$. Show that: $$2(DF+EF)\ge BC$$

maybe use cosine theorem,let $\dfrac{BD}{AB}=k,AB=c,BC=a,AC=b$, and in $\Delta ABC$ we use cosine theorem we have $$a^2=b^2+c^2+bc\tag{1}$$ and $$DF^2=BD^2+BF^2-2BD\cdot BF\cos{\angle B} =(kc)^2+\dfrac{a^2}{4}-2kc\cdot\dfrac{a}{2}\dfrac{a^2+c^2-b^2}{2ac}=k^2c^2+\dfrac{a^2}{4}-\dfrac{k(a^2+c^2-b^2)}{2}$$ the same as $$EF^2=\dfrac{a^2}{4}+(kb)^2-\dfrac{k(a^2+b^2-c^2)}{2}$$ it is equivalent

$$\sqrt{4k^2c^2+a^2-2k(a^2+c^2-b^2)}+\sqrt{4k^2b^2+a^2-2k(a^2+b^2-c^2)}\ge a,0\le k\le 1\tag{2}$$

I have tried some inequality (AM-GM,Cauchy-Schwarz,$\cdots$) to prove $(2)$, but didn't see the solution.

Answer 1

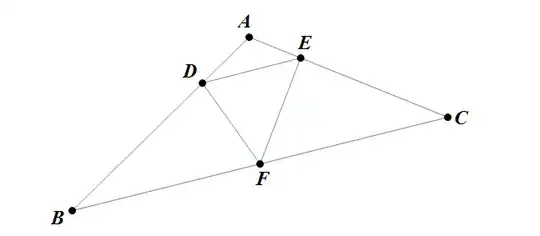
As you did, let us set $k:=BD/AB$.

If $1/2\le k\lt 1$, then letting $M,N$ be the midpoint of the side $AB,AC$ respectively, we have $$2(DF+EF)\gt 2DE\ge 2MN=BC$$

In the following, we consider the case when $0\lt k\lt 1/2$.

By the law of cosines, $$BC^2=AB^2+AC^2-2AB\cdot AC\cos\angle{BAC}\iff a^2=c^2+b^2+cb\tag1$$

By the way,

$$2(DF+EF)\ge BC$$ is equivalent to $$2DF\ge BC-2EF$$ Since both sides are non-negative, this is equivalent to $$4DF^2\ge BC^2-4BC\cdot EF+4EF^2$$ which can be written as $$4BC\cdot EF\ge (BC+2DF)(BC-2DF)+4EF^2$$ Since $BC-2DF\ge 0$, the both sides are non-negative, and so this is equivalent to $$(4BC\cdot EF)^2\ge ((BC+2DF)(BC-2DF)+4EF^2)^2,$$ i.e. $$8BC^2\cdot EF^2-BC^4-16EF^4-16DF^4+8BC^2\cdot DF^2+32EF^2\cdot DF^2\ge 0$$

Using that $$4DF^2=4k^2b^2+a^2-2k(a^2+b^2-c^2)$$ $$4EF^2=4k^2b^2+a^2-2k(a^2+b^2-c^2)$$ this is equivalent to $$2a^2(4k^2b^2+a^2-2k(a^2+b^2-c^2))-a^4-(4k^2b^2+a^2-2k(a^2+b^2-c^2))^2-(4k^2c^2+a^2-2k(a^2+c^2-b^2))^2+2a^2(4k^2c^2+a^2-2k(a^2+c^2-b^2))+2(4k^2b^2+a^2-2k(a^2+b^2-c^2))(4k^2c^2+a^2-2k(a^2+c^2-b^2))\ge 0,$$ i.e. $$16k^4(b^2-c^2)^2-32k^3(b^2-c^2)^2-8k^2(a^2(b^2+c^2)-2(b^2-c^2)^2)+8a^4k-3a^4\color{red}{\le} 0$$

Here, let $$f(k):=16k^4(b^2-c^2)^2-32k^3(b^2-c^2)^2-8k^2(a^2(b^2+c^2)-2(b^2-c^2)^2)+8a^4k-3a^4$$ So, we want to prove that $f(k)\le 0$ for $0\lt k\lt 1/2$.

Now, $$f'(k)=64(b^2-c^2)^2k^3-96(b^2-c^2)^2k^2-16(a^2(b^2+c^2)-2(b^2-c^2)^2)k+8a^4$$ $$\begin{align}f''(k)&=192(b^2-c^2)^2k^2-192(b^2-c^2)^2k-16(a^2(b^2+c^2)-2(b^2-c^2)^2)\\&=192(b^2-c^2)^2\left(k-\frac 12\right)^2-16a^2(b^2+c^2)-16(b^2-c^2)^2\end{align}$$

With $f''(1/2)\lt 0,f'(0)\gt 0$ and $$f'\left(\frac 12\right)=8a^2(a^2-b^2-c^2)\gt 0$$ we know that $f(k)$ is increasing for $0\lt k\lt 1/2$, and using $(1)$ gives $$f\left(\frac 12\right)=-3b^2c^2\lt 0$$

It follows from this that $f(k)\le 0$ for $0\lt k\lt 1/2$. $\blacksquare$

Answer 2

This is not a complete solution, just some simplification.

Square both sides of (2) and using (1) to get rid of $a^2$, we obtain:

$$2\sqrt{c^2+b^2(1-2k)^2+bc(1-2k)}\sqrt{b^2+c^2(1-2k)^2+bc(1-2k)}+((b^2+c^2)(1-2k)^2+2bc(1-2k))\ge bc\tag{3}$$

Let $\kappa=1-2k$, thus $-1\le \kappa \le 1$. Then (3) becomes $$2\sqrt{c^2+b^2\kappa^2+bc\kappa}\sqrt{b^2+c^2\kappa^2+bc\kappa}+((b^2+c^2)\kappa^2+2bc\kappa)\ge bc\tag{4}$$