I think I was able to solve my doubt. I wrote the answer here, but I'll type it down here:
So first of all the difficult point is to show that the AHSS collapses at the second page. After that it is almost trivial. In order to prove it, the hypothesis on orientation will be of main importance.
Let me fix some notation: $ i_n \colon \mathbb{C}P^n \to \mathbb{C}P^{\infty}$ is the usual inclusion, and $ y_E$ is the image of the orientation class in the unreduced second cohomology group of $\mathbb{C}P^{\infty}$.
The first step is to identify a certain element in the AHSS for $ \mathbb{C}P^1$ with the orientation $ i_1^* y_E$. Recall that $ H^*(\mathbb{C}P^n)\cong \mathbb{Z}[y]/(y^{n+1})$
Claim 1: The element $ y \otimes \imath \in E^{2,0}$ represents the orientation class $ i_1^*(y_E)$.
Proof of Claim 1: Consider the AHSS for $\mathbb{C}P^1$:
Since the edge homomorphism for the AHSS is always surjective, we have that the only possible non-zero differentials (the differentials of the 2nd page starting from the zero-th column to the second one) are trivial. This implies that the spectral sequence collapses. Since the second page is generated multiplicatively by $ y\otimes \imath \in E^{2,0}_2$ and it is a free graded $ \pi_*E$-module (i.e. the extension problem is trivial) the isomorphism $ E^2(\mathbb{C} P^1)\xrightarrow{\cong} E^{0,2}_2 \oplus E^{2,0}_2$ maps $ i_1^*(y_E) \mapsto y \otimes \imath$ ( $ E_2^{0,2} =E^2(\ast) $ and the other is the reduced cohomology group).
Claim 2: The AHSS for $ \mathbb{C} P^n$ collapses at the second page and we have that $ y \otimes \imath \in E_2^{2,0}$ represents the orientation class $ i_n^*(y_E)$
Proof of Claim 2: Let us have a look at the AHSS for $ \mathbb{C} P^n$:
Since the AHSS is multiplicative and thanks to the ring structure of the second page, it's enough to show that the element $ y \otimes \imath \in E_2^{2,0}$ is an infinite cycle. In fact, one proceed inductively using the fact that any other element in the previous page (i.e. in the second page) is a $ \pi_*E$-linear combination of powers of $ y\otimes \imath$. Consider the inclusion $ i_1^n \colon \mathbb{C} P^1 \to \mathbb{C} P^n$. We know that $ i_n^*(y_E)$ is sent to $ i_1^*(y_E)$ by the fact that $ (i_1^n)^*i_n^*=i_1^*$. Now recall that $ i_1^n$ induces a map of spectral sequences. Since we know that AHSS for $ \mathbb{C} P^n$ converges a priori to $ E^*(\mathbb{C}P^n)$ ($ \pi_*E$ is required to be bounded below by Kochman and Adams in another chapter) there is an element in the stable page $ E_{\infty}^{p,q}$, for some $ p,q \in \mathbb{Z}$ which is a representative of $ i_n^*(y_E)$.
By Claim 1, we already know that the representative of $ i_1^*(y_E)$ lies in $$ E_{\infty}^{2,0}\cong F^2 E^2(\mathbb{C} P^1)/F^3 E^2(\mathbb{C} P^1)$$ Now suppose that the class of $$ i_n^*(y_E)\in F^p E^{p+q}(\mathbb{C} P^n)/F^{p+1} E^{p+q}(\mathbb{C} P^n)$$ since the inclusion preserves the filtration, it would send our class to an element lying in $ F^p E^{p+q}(\mathbb{C} P^1)/F^{p+1} E^{p+q}(\mathbb{C} P^1)$, but since we already established that the image of $$ i_n^*(y_E)\in F^2 E^2(\mathbb{C}P^1) / F^{3} E^2(\mathbb{C}P^1)$$ it must be that $ p\geq 2$ and $ q=0$ (Since $ F^pE^2(\mathbb{C} P^n)\subseteq F^{p-1}E^2(\mathbb{C} P^n)$). By definition of the filtration for the cohomological AHSS, if this element lies in $ F^p E^2(\mathbb{C}P^n) / F^{p+1} E^2(\mathbb{C}P^n)$ for $ p>2$ in particular its representatives lie in $$ F^2 E^2(\mathbb{C}P^n)$$ meaning that when restricted to $\mathbb{C}P^1$ they are all zero (it is crucial here that the inclusion identifies the 2 skeleton of $ \mathbb{C}P^n$ with $ \mathbb{C}P^1$). Since we know that the restriction to $ \mathbb{C}P^1$ of the orientation $ i_n^*(y_E)$ is a non-zero element, it must be $ p=2$ and $ q=0$. This shows that we have to look for a representative for $ i_n^*(y_E)$ in $E_{\infty}^{2,0}$. Consider the following diagram, where $ E_r'^{p,q}$ will denote the group in position p,q, page r of the AHSS for $ \mathbb{C}P^n$:
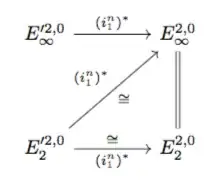
The lower map is an isomorphism since it is the map induced between the second singular cohomology groups of $ \mathbb{C} P^1$ and $ \mathbb{C} P^n$. The diagram implies that the unique preimage of the representative of $ i_1^*(y_E)\in E^2(\mathbb{C}P^1)$, which by Claim 1 is identified $ y \otimes \imath$, can only be the element $ y \otimes \imath$ in $ E_2'^{2,0}$, and therefore it has to be an element of $ E_{\infty}'^{2,0}$ i.e. an infinite cycle. This readily implies that the AHSS collapses at the second page, since it is multiplicative: the second page is generated multiplicatively by $ y \otimes \imath$, and we just showed that it is an infinite cycle, by an easy inductive reasoning we have that the differentials in every page must be zero since they are $ \pi_*E$-linear derivations.
In conclusion:
Since the stable page is a free graduated $ \pi_*E$ module, the extension problem is trivial (all the s.e.s. splits). In fact one can organise all the s.e.s. in the following $$ 0 \to F^{p+1}E^{p+\bullet}\to F^pE^{p+\bullet} \to E^{p,\bullet}_{\infty} \to 0$$ (see here for example) and therefore if the latter is a free graded module, the s.e.s. splits.
Therefore we have an isomorphism of $ \pi_*E$-modules $ E^m(\mathbb{C}P^n) \cong \bigoplus_{p+q=m}E_{2}^{p, q}$.
Using the fact that AHSS is multiplicative, and the ring structure on the stable page is the one one would expect to have, by compatibility of the two product structures (by axiom of multiplicative spectral sequence) and the above iso we have the claim
Maybe it's not the most elegant solution but I think it does the job: it was not so obvious as many references claimed. I'd love to see if there are more elegant proofs
