8

Note: in relation to the answer of the duplicate question, I see that the second picture below refers to the triangulation when we consider simplicial complexes. I do not understand why the triangles are used as they are, however, so would like some help trying to understand this

I am having a lot of trouble understanding triangulations. I know that a triangulation involves decomposing a 2-manifold into triangular regions.

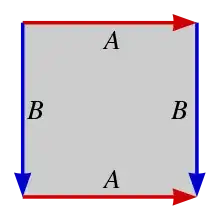
A common example is the torus, which can be constructed from the square. I understand this representation:

Torus

Since the torus is homeomorphic to the space obtained by identifying those edges together.

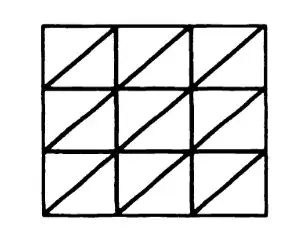
What I do not understand is the triangulation given:

Torus

Why is this triangulation given in all the books and resources etc?

I do not understand what all the triangles mean. Why could we not just split the square into 2 triangles?

Many thanks for your help on this one

Michael Albanese
  • 104,029
thinker
  • 2,229
  • 1
  • 27
  • 52
  • Possible duplicate of Triangulation of Torus – zibadawa timmy May 05 '16 at 12:47
  • I know that there are a fair few examples of a triangulation of a torus but I couldn't one with an explanation of what is going on on a fundamental level, and why the triangles are as they are. Yes that question is on the same subject matter, but does not solve my problem at all – thinker May 05 '16 at 12:54
  • Your "question" is literally "Why is this triangulation given in all the books and resources etc?". You then follow up by asking "Why could we not just split the square into 2 triangles?". The linked duplicate patiently explains that (1) you can split the square into two triangles, and this is useful for some purposes, and (2) that as a matter of definition, two triangles is not enough to represent the torus as a "simplicial complex". Please improve your Question to present a more specific "problem" concerning "why the triangles are as they are". – hardmath May 05 '16 at 13:23
  • My main question is can someone help me understand the basics behind what is going on and I did not find the other question useful for me. I understand the second case is for simplicial complexes, that is what I want to work with. But I do not understand why these triangles were used – thinker May 05 '16 at 13:25

2 Answers2

10

In a triangulation (specifically, a simplicial complex), the three vertices of a triangle are distinct. (Technically, the two 0-cells at the boundary of each 1-cell are distinct, the three 1-cells at the boundary of each 2-cell are distinct, et c. This leads to: the vertex set of a $k$-cell contains $k-1$ distinct vertices.) That is, if I tell you three vertices you can immediately tell me that either "there is no triangle with those three vertices" or "there is exactly one triangle with those three vertices, and its that one". (More generally, given a list of $k$ vertices, you can tell me whether there is no $k-1$-cell with those vertices or there is exactly one such $k-1$-cell and it's that one.) The intention is to make the vertex set of a $k$-cell into a unique label for the cell.

If you divide the square in half, there is only one vertex after the identification of the labelled edges. This fails "distinctness". Call the one vertex, $v$. Both triangles have the same vertex collection, "$v,v,v$", so giving a valid vertex set does not pick out a single triangle.

Eric Towers
  • 70,953
  • OK I think that makes sense to me - So if I had just cut the square into two triangles, I am topologically reducing it down to only one triangle. But why does the correct triangulation (second picture) have so many triangulation? – thinker May 05 '16 at 12:58
  • @thinker Check the definition of triangulation you are using. The triangulation you want to use is an example of a CW complex. The triangulation you see often given is an example of simplicial complex. It turns out either one works just as well as the other for most purposes, but that takes some time to establish. In this case, pay attention to requirements of injectivity and how many "vertices" and "edges" a triangle is supposed to have versus what your attempt at a triangulation would actually yield in the quotient space. – zibadawa timmy May 05 '16 at 13:01
  • 1
    No. It's two triangles, but they both have the same vertex set. Why don't you take the $2 \times 2$ (8 triangles) in the lower right corner of the diagram and label the vertices. You'll discover that you have pairs of triangles with the same vertex sets. – Eric Towers May 05 '16 at 13:04
2

Hint: What are the images of the corners of the big square in the quotient?

See also this Q&A (and the comments), where the poster makes much the same mistake.

Community
  • 1
zibadawa timmy
  • 4,533
  • So in the second picture, the simplices are 'embedded' but I do not understand what this means. – thinker May 05 '16 at 12:56
  • @thinker As is mentioned in the linked Answer and comments, "embedded" is topology/geometry speak for "continuous injection" (or possibly smooth injection). Your triangulation doesn't yield a continuous injection of the triangles, and indeed the intersection of the triangles in the quotient space violates the definition you're likely using for "triangulation". – zibadawa timmy May 05 '16 at 13:03
  • In a simplicial complex we want simplices that meet "face to face" (edge to edge or corner to corner in the case of triangles). Having a triangle share all three edges (and all three corners) with another triangle makes the quotient space kind of pathological. – hardmath May 05 '16 at 19:51