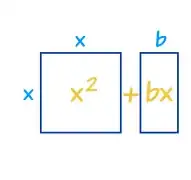4

I was just reading this MathisFun article on completing the square. It states that geometry can help complete the square. It starts off with a square and a rectangle (pictures come from link):

Completing the square 1

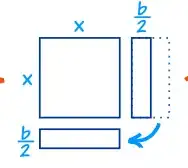
Then, it cuts $b$ in half, and moves it under the $x^2$ square:

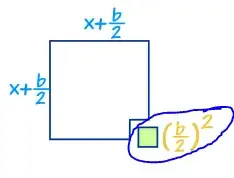
enter image description here

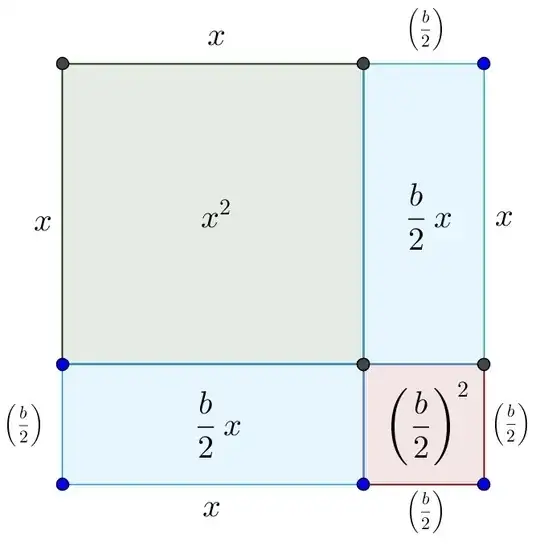
Now, the square is "nearly completed", but it has this part that completes the square that equals $\left(\frac b2 \right)^2$ (circled in blue):

enter image description here

My question is, where did that part come from, and why does it equal $\left(\frac b2 \right)^2$. The article doesn't give me a reason and there are no other sources as to why.

Obinna Nwakwue
  • 1,098
  • can you expand $(x+b/2)^2$ please ? and the target is to find $C$ and $\rho$ such that $x^2 + bc + C = (x+\rho)^2$ – reuns Apr 21 '16 at 21:33
  • 2
    The picture describes the situation perfectly. What is unclear ? The green part is needed to complete the big square, and it is obvious that the sides have length $b/2$ – Peter Apr 21 '16 at 21:35
  • 1
    After you add the horizontal and vertical rectangles to the $x$ by $x$ square (shown in your first figure), notice that there is a gap (see the arrow in your first figure) that is a square with sides of length $\frac{b}{2}.$ The area of this square is length times width . . . – Dave L. Renfro Apr 21 '16 at 21:35
  • You can say that as an answer; that will help me. – Obinna Nwakwue Apr 21 '16 at 23:04
  • Regarding "You can say that as an answer ...", I don't know which of the three people who made a comment you are referring to, but Steven Gregory's answer seems perfectly appropriate to me and I'm upvoting it. (For some reason, it has no upvotes thus far, 11 hours after he posted it.) – Dave L. Renfro Apr 22 '16 at 13:01
  • @DaveL.Renfro, I was referring to your answer, but I've already seen one. – Obinna Nwakwue Apr 22 '16 at 20:39

1 Answers1

4

$\left(x + \dfrac b2 \right)^2 = x^2 + 2\left( \dfrac b2 x \right) + \left( \dfrac b2 \right)^2 = x^2 + bx + \dfrac{b^2}{4}$

Completing the square

Steven Alexis Gregory
  • 27,619