I understand that for a system to behave chaotically, it needs to be "topologically mixing". However, I am not sure what that term really means.
There are several explanations of this online. Thought, I haven't found an explanation for the layman.
What is the meaning of the term "topologically mixing"?
I'm assuming you've seen the definition:
A dynamical system $f$ on $X$ is said to be topologically mixing if for every two open set $U$ and $V$ in $X$, there is $N$ sufficiently large that $f^n(U)\cap V\neq\emptyset$ for all $n\geq N$.
This means that I can choose any two open sets, and then iterate one of them so that after a certain point, its image intersects the other for every iteration. To see why this is nontrivial, note that we can extend the definition for any finite number of open sets: $U$, $V_1,...,V_n$. I can iterate $U$ by $f$ enough times that its image eventually intersects all of the sets $V_1,...,V_n$ simultaneously! Even if the $V_i$ sets are really far apart. This in order to accomplish this, $f$ has to either make $U$ really big, or stretch, fold, and twist $U$ so that its image eventually permeates the space it lives in.
Here are some pictures to illustrate this behavior. Here are my two sets $U$ and $V$:
Now I iterate $U$ a bunch of times:
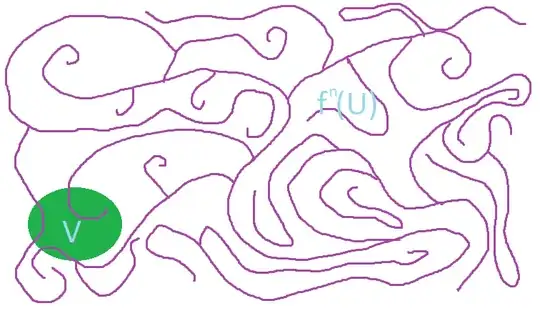
The image of $U$ under iteration becomes wild, and intersects $V$. If this system is indeed topologically mixing, the image of $U$ will continue to intersect $V$ for all subsequent iterations.
