A spiralling sequence based on integer divisors. Has anyone noticed this before?

Question

Firstly, please excuse the informal style of my explanation, as I am not a mathematician, although I am aware that this can be explained in more formal terms.

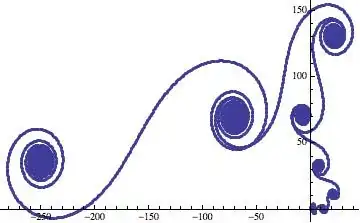
I have mapped integers to points on a circle on the complex plane in the following way: $$ a_n=\prod _{j=1}^n (-1)^{2 (n \bmod j)/j} $$ I then took a sequence of partial sums of $a_n$: $$ b_n=\sum _{j=1}^n a_j $$ I think of it as a path made of vectors of length 1 on the complex plane. I then plotted $b_n$, and I saw this beautiful vine-like shape:

(for $n <= 45000$)

(for $n <= 1000$)

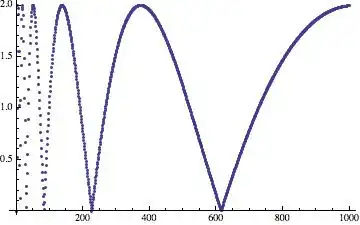
The path goes clockwise, then the spin accelerates until it turns anticlockwise and moves somewhere else. In order to find out more about the "whirlpools" and "peak flows", I checked the differences between consecutive terms of $a_n$, and obtained the following plot:

The minima/"peak flows" fall at $n = 1, 4, 11, 30, 83, 226, ...$, which appears to correspond to http://oeis.org/A078141, and to be given by $$\left\lfloor e^{n-\gamma }\right\rfloor$$ I have checked that the "whirlpools" appear to correspond to $$\left\lfloor e^{n - \gamma + 1/2}\right\rfloor$$ I think this would mean that each branch of the vine is $e$ times larger than the previous one in some way...

As for the position of the "peak flows" on the complex plane, they are: $$ 1.,0.5\, +0.866025 i,0.695702\, +1.84669 i,1.28152\, +1.03625 i,1.75407\, +1.91755 i $$

for $n = 1, 4, 11, 30, 83$.

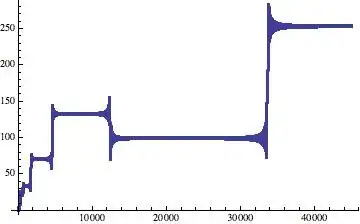
Here is a plot of the absolute values of $b_n$:

Here is an array plot of distances between terms of $a_n$, for $n <= 100$, just for fun, really:

I have a bunch of questions:

• As per title. Is this something that has been noticed before?
• Why do the "whirlpools" fall where they do on the complex plane? What is special about those values?
• Is every term of $a_n$ unique? If so, is it possible that there exists a way of learning something about the divisors of $n$ from $a_n$ or $b_n$?

Answer 1

For the first question: You may be able to find some similar results on exponential sums in the book "Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis," by Montgomery. Also, Noam Elkies has a similar picture in part of his analytic number theory course.

For the second question: "Why do the whirlpools occur where they do?" Let us first simplify the problem a little: to avoid confusion regarding which root to use in the definition of $a_n$, take $a_n=\prod_{j=1}^n e^{2\pi i(n\pmod{j})/j}$ Now, observe that: $a_{n+1}=a_n\cdot e^{\frac{2\pi i n}{n+1}}\cdot\prod_{j=1}^{n+1}e^{2\pi i/j}=a_n\cdot e^{\frac{-2\pi i }{n+1}}\cdot\prod_{j=1}^{n+1}e^{2\pi i/j}$ (if you would like me to write out a proof of this 'observation,' leave a comment, and I'll add one). Then, by induction and the fact that $a_1=1$, we obtain the explicit formula: $a_n=\prod_{m=0}^{n-2}\prod_{j=1}^{m+1}e^{\frac{2\pi i}{j}}$, which we can simplify down to: $$a_n=\exp(2\pi i nH_n)$$ where $H_n=\sum_{j=1}^n\frac{1}{j}$. Then we may compute $a_{n+1}-a_n=\exp(2\pi i(n+1)(\frac{1}{n+1}+H_n)-\exp(2\pi inH_n)$ $=\exp(2\pi inH_n)\exp(2\pi iH_n)-\exp(2\pi inH_n)=a_n(\exp(2\pi i H_n)-1)$

Note that a whirlpool will correspond to the smallest possible change $|a_{n+1}-a_n|$: we are looking for places where adding consecutive terms does not change things by very much. So, using the approximation $H_n\approx \log n+\gamma$ helpfully pointed out by Marc Paul in the comments above, we get that the local minimums of $|a_{n+1}-a_n|$ should occur near $\exp(2\pi i (\log(x)+\gamma))=1$ i.e. when $\log(x)+\gamma=n$ for some integer $n$, and this occurs exactly when $x=e^{n-\gamma}$. This is because then $|a_{n+1}-a_n|\approx 0$ will be as close to $0$ as possible. Similarly, the "maximum flows" should be near where $\exp(2\pi i(\log(x)+\gamma))=-1$, i.e. near $x=e^{n-\gamma+.5}$, because this is where $|a_{n+1}-a_n|\approx 2$, which is the maximum possible value.

Warning: there is a little unfinished business ahead in the answer to your third question, "Is every term of $a_n$ unique?" In short, no. $a_1=1=a_2$. However, in general if $a_n=a_m$ with $n>m$, then using our formula for $a_n$, we have $\exp(2\pi inH_n)=\exp(2\pi imH_m)$ which implies $2\pi inH_n-2\pi imH_m=2\pi i k$ for some integer $k$. Then we have: $$\sum\limits_{j=1}^m\frac{n-m}{j}+\sum\limits_{j=m+1}^n\frac{n}{j}=k$$ which I suspect has no solutions other than $n=2$, $m=1$, $k=2$, but which remains to be proved.