I saw this question which had a similar viewpoint, but was limited to straight lines and polynomials. Now we know that we can graph some pretty crazy stuff with parametric equations. For example: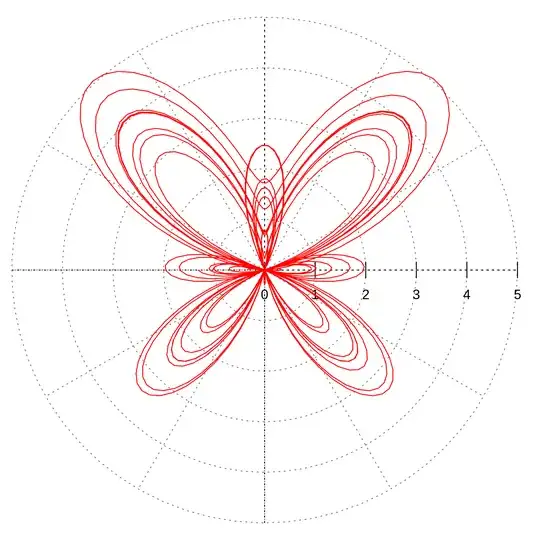 
and even
So naturally one would think that, if we put pen to paper, and drew something, anything, there would be a set of parametric equations to describe that shape or figure (of course, I'm not saying that finding the equations will be easy, but they should exist). So, is this true?
As far as I know, yes. Just about any line you could draw could be approximated by a parametric curve consisting of polynomials. For the Cartesian equivalent, look up "infinite series polynomials". A higher degree of accuracy can be achieved by adding more polynomial terms. Cusps (corners) could be achieved by including such functions as $\sqrt{x^2}$. Jump discontinuities could be achieved by including such functions as $\sqrt{x^2}/x$. A single parametric curve could then look as if it was multiple lines.
Disclaimer: All equations produced this way would be approximations of the originally drawn line, but could be made arbitrarily accurate. Coming up with these functions could be extremely tedious to do by hand, because any change made to any portion of the function would require adjustments to the rest of the curve.
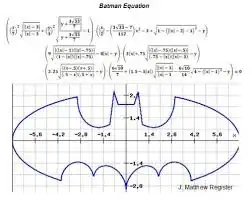
If you look at this image, an answer becomes a lot more apparent. You can define as many separate functions as you like over whatever intervals you like and adjoin them to each other by the "endpoints" of the intervals to get whatever shapes you like.
– Edward Evans Mar 19 '16 at 05:03