I did a (non-rigorous) analysis based on residuals on the plane Im[z]>0.
Let $C$ be the contour that runs from $-a$ to $a$ (in a straight line over the real axis), and back over the semi-circle $|z|=a$ with $Im[z]\ge0$, see the image (taken from Wikipedia) below.
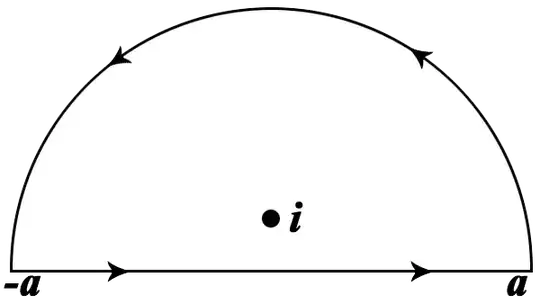
Inside this contour, the integrand is analytical, except for a finite number of poles: the pole on $z=-1+2i$ due to the first factor, and the poles on $z=2\pi n$ for $n=1,2,...,N$ due to the second factor. Here, $N$ is the biggest integer such that $2\pi N<a$. There is also one pole exactly on the contour, at $z=0$.
According to the residue theorem, the contour-integral over C can be calculated by summing the residuals of these poles, and multiplying this by $2\pi i$. (Don't forget, here and later, that the pole at $z=0$ only counts half, because the contour goes right through it.)
Now, let $a$ go to infinity. This also means that $N$ will go to infinity. If the contribution of the semicircle part of the contour goes to zero, all that is left is $I$. (I have no proof that the contribution goes to zero. In fact, I have some doubts for $z\rightarrow i\infty$... But since the result later on seems to agree to numerical values, I ignore this, and I guess it could be made rigorously by restricting $R$ to values such that the contour falls in between the poles and not on the poles.)
The poles at $z=2n\pi i$ generate an infinite sum, that converges. I put this sum in Wolfram Alpha, and this showed that the sum can be written with digamma functions. The pole at $z=-1+2i$ gives one extra term. Altogether, the result is:
$$I=-\frac{\pi}{5} i -\frac{i}{4}\left(\psi\left(1-\frac{(1+\frac{i}{2})}{\pi}\right)-\psi\left(1+\frac{(1-\frac{i}{2})}{\pi}\right)\right)-\frac{\pi}{2-2e^{1-2i}}.$$
where $\psi$ is the digamma function. It can be simplified a little bit further by using the recurrence relation $\psi(1+x)=\psi(x)+1/x$ and the reflection formula $\psi(1-x)=\pi\cot(\pi x)+\psi(x)$.
Although the expression for $I$ has the imaginary unit $i$ in it, it is a real number.
According to wolfram alpha, it evaluates to -0.383448111064056808053521526581710702474772465557555272482. This corresponds to the other answers found numerically here, so I trust that this analysis can be made rigorously.
I tried if the digamma terms could be simplified, as there seems to be a nice symmetry in it, but I could not see how to really make it more simple.

syms z;f=1/(((z+1)^2+4)*(exp(-z)-1));I=vpa(int(f,z,-Inf,Inf)). Usedouble(I)to convert the result back to floating point if you like. – horchler Mar 11 '16 at 15:34