1

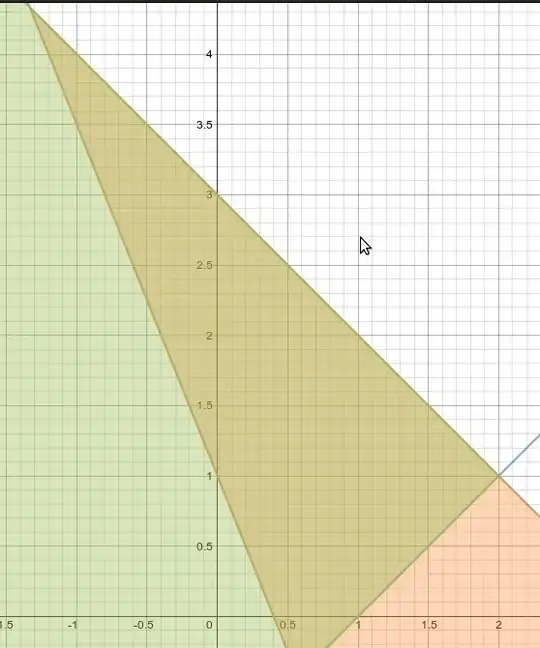
Let be the following linear program:

\begin{equation*} \begin{cases} \max f(x_1,x_2) =3x_1+2x_2\\ 5x_1 + 2x_2 \ge 8\\ x_1 - x_2 \le 1\\ x_1 + x_2 \le 3\\ x_1,x_2\ge 0 \end{cases} \end{equation*}

enter image description here

I know how to graphically guess where a starting point is but how to find it with the Simplex algorithm?

Here I graphically guess that we would strat from the bottom or the left, but it's only a guess as fas as we are under a $\max$ condition.

After having put in place the begining of the Simplex algorithm, I have:

$$ \begin{array}{llllll} x_3= 8& -5X_1 &-2X_2 & & &\\ x_4= 1& - X_1& +X_2& &\\ x_5= 3& -X_1 & -X_2 & & &\\ \hline z= & 3X_1 & + 2X_2 \end{array} $$

but how to find the starting point from here? I only know that the variable about to come is $X_1$ because it has the greatest coefficient...

Revolucion for Monica
  • 1,541
  • take a look at any linear programming course or at https://en.wikipedia.org/wiki/Simplex_algorithm#Finding_an_initial_canonical_tableau – reuns Mar 03 '16 at 17:40

1 Answers1

1

You need to solve another linear problem before hand in other to find a feasible solution: $$ \mbox{Minimize }\;Z= t $$ subject to $$ 5x_1+2x_2+t\ge 8\\ x_1-x_2\le 1\\ x_1+x_2\le 3\\ x_1,x_2,t\ge 0 $$ The optimal solution of this problem will give you a tuple $(x_1,x_2,t)=(x_1^*,x_2^*,0)$ which is a valid starting point. If you get an optimal solution with $t>0$, the initial problem is not feasible.

Kuifje
  • 9,802