Consider the second order differential equation $ x'' + f(x)x' + g(x) = 0 $ with $$ f(x) = -\lambda + x^2, \quad g(x) = (-1 + x^2)x \, . $$ with $\lambda > 0$.
Note: The original post had a misprint in this formula. $g$ should be a cubic, not a quadratic.
This has the general form of Lienard's equation. Much is known about the asymptotic behavior (as $t \to \infty$) of solutions, if $g(x) = (1 + x^2)x$. Essentially, all non-constant solutions must either lie on a limit cycle (which is unique) or converge to this limit cycle.
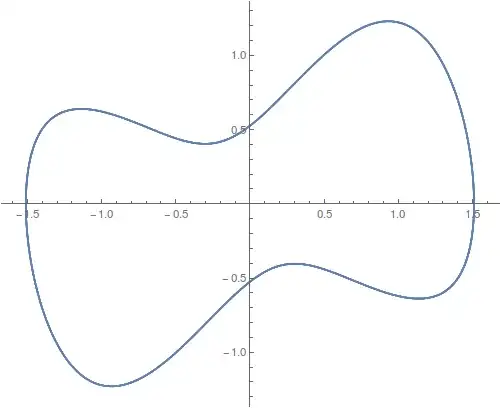
However, in the form given above, there are stationary points at $x = \pm 1$ that are stable if $\lambda < 1$, there is a Hopf bifurcation as $\lambda$ increases past $1$, and numerical evidence suggests that there are unstable limit cycles coexisting with stable large amplitude limit cycles for some $\lambda < 1$. An image of the stable limit cycle for $\lambda = .772$ is shown below. So the picture is more complicated.
Is anything known about the global behavior of solutions for this type of problem?