How can I draw plane distributions in $\mathbb{R}^3$?

Question

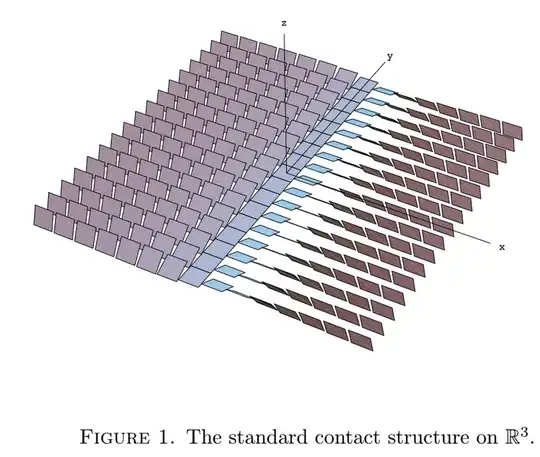
I see so many nice pictures of contact structures, integrable plane distributions, etc., in manuscripts and online and I have absolutely zero idea how they're made. For example, the following image was posted on Tumblr (source unknown):

I was able to gather some information online.

For instance, if I go to the Wikipedia page on Contact geometry, there's an image of a contact structure on $\mathbb{R}^3$, the notes on which say Generated with MetaPost and Inkscape. I have some experience with Inkscape but ideally, I'd like to find a solution that can take a form (e.g. $dz - y dx$ for the Wiki picture) and automate the drawing without me having to draw a hundred little rectangle "planes" and manually position them, etc.

I also took look through the online Mathematica documentation to see what was available there...I'm sure there's a solution out there, but without asking someone, I just can't seem to find it on my own.

Any information would be hugely appreciated!

@PVAL - I'm not sure that Mathematica is the software I need, though, so I figured this was a worthwhile first step. Is Mathematica something you think could work? — cstover, Feb 28 '16 at 20:59
That was really just a suggestion if this doesn't work out. There are more people over there with better mathematica experience in my opinion. — PVAL-inactive, Feb 28 '16 at 21:47
@PVAL - Great suggestion! I'll keep an eye here for the day or two and then close here / repost there if nothing pans out! Many thanks! — cstover, Feb 28 '16 at 22:11

score 4 · Accepted Answer · answered Mar 01 '16 at 05:30

4

I doubt you'll find a ready-to-go solution for this type of plot - odds are you'll have to roll your own to some extent. Here's a quick starting point in Mathematica:

SlopeSquare[x_, y_, xs_, ys_, size_: 1, z_: 0] := With[{
    x1 = x - size, y1 = y - size, x2 = x + size, y2 = y + size, 
    pt = ({#1, #2, z + xs (#1 - x) + ys (#2 - y)} &)}, 
    Polygon[{pt[x1, y1], pt[x1, y2], pt[x2, y2], pt[x2, y1]}]]

Graphics3D[Flatten@Table[
    SlopeSquare[x, y, -y, 0, 0.09], {x, -2, 2, 0.2}, {y, -2, 2, 0.2}], 
    PlotRange -> {All, All, {-2, 2}}, Boxed -> False]

It's pretty rough - for example these rectangles are drawn with constant projection onto the x-y plane rather than with constant size, and it only works for forms of the form $dz + \texttt{xs} dx + \texttt{ys} dy$. Hopefully you get the idea and can work out how to tweak it to your liking.

answered Mar 01 '16 at 05:30

Anthony Carapetis

36,533

Wow, thank you so much! I'm about 100% sure that this will end up being the best answer, but I'm going to give it a couple more days to see if anything else pans out. Seriously, though: This is absolutely phenomenal! I cannot thank you enough! – cstover Mar 01 '16 at 18:29
$dz + \texttt{xs} dx + \texttt{ys} dy$ What does this mean? Can you get something like a standard contact structure such as $dz+ydx$? – PVAL-inactive Mar 02 '16 at 00:00
@PVAL: xs, ys are the "slope" arguments to SlopeSquare which you can specify for each "square". My example above has $\texttt{xs}=-y,\texttt{ys}=0$ for the square centred at $(x,y)$ and thus I've plotted $dz - y dx$. (Actually I think I'm slightly off - the correct formula is probably $dz - \texttt{xs }dx - \texttt{ys} dy$, so I think I've in fact plotted exactly $dz + y dx$.) – Anthony Carapetis Mar 02 '16 at 00:06

How can I draw plane distributions in $\mathbb{R}^3$?

1 Answers1