12

The isohedra have identical faces. They have symmetries acting transitively on their faces -- any face can be mapped to any other face to give the same figure.

There are also polyhedra where all faces are the same, but the faces are not transitive. For example, take an antiprism and make caps with the same triangles.

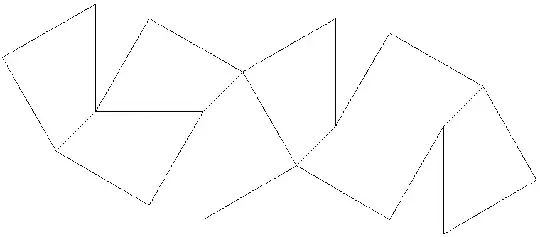
I just found that this net seems to work, with all faces identical. The long edges all have length 1, with angles of 60 and 90 degrees.

not an isohedron

Have polyhedra like this been explored? Is there a name for non-isohedra where all faces are the same?

Ed Pegg
  • 21,868
  • I would love to see a 3D rendering of this shape. I can't immediately judge from the net whether if actually fits together. – M. Winter Oct 31 '20 at 23:21
  • @M.Winter it's one of the member of the trapezohedron family (a particulalry distorted one) – ARG Apr 03 '22 at 19:38
  • @ARG Are you sure? Looking up trapezohedron it seems there are two vertices (top and bottom) at which all incident interior angles are equal. I can't find these distinguished angles in the net in the post. – M. Winter Apr 03 '22 at 19:45
  • @M.Winter indeed, it's not a trapezohedron in that sense. I think the standard definition of trapezohedron do require that they are isohedral (whereas the above is only monohedral). The above figure only has two different type of faces (based on the angle they have at the tip) so it's still very close to one. – ARG Apr 03 '22 at 19:58

1 Answers1

7

I just posted a question about these polyhedra, which are monohedral but not isohedral. I've included your shape in the question, which seems to have been unknown at least prior to 1996. I've included every example I know of there, though I very much doubt it encompasses all known non-isohedral convex monohedra.

RavenclawPrefect
  • 18,328
  • This seems more like a comment than an answer. – M. Winter Oct 31 '20 at 23:20
  • 2
    Thanks for the feedback. I waffled between the two, and went with giving an answer because the question does explicitly ask what these shapes are called, and I think the linked question answers "have these polyhedra been explored" about as well as can be done from the available literature. (It also seemed like there were unlikely to ever be other answers given to this question.) Is there a better guideline I should use for determining whether to post a comment vs. an answer? (I can delete this answer and repost it as a comment, if that seems worthwhile.) – RavenclawPrefect Oct 31 '20 at 23:34
  • 1
    It is hard to give a clear rule. You are right, you stated the correct term for these polyhedra, which I first missed, and this may qualify as an answer. But advertising another question is often better placed in a comment (maybe separate this from the answer?). I flagged this answer, and I would say: let the community decide. My comment was just my opinion. If you are new to the network (and I don't know whether you are), don't worry, it probably takes some time to know what belongs where :) – M. Winter Oct 31 '20 at 23:47
  • @RavenclawPrefect was it really not known that the trapezohedra (even when fixing the number of faces) come in a infinite family of members? this certainly how people produced the "skew dices" so It seem it should have been known for a while... – ARG Apr 03 '22 at 19:40
  • @ARG: This is not a trapezohedron; it is not face-transitive, as stated in the original post. – RavenclawPrefect Apr 03 '22 at 21:35