Summing over components of a basis: Coalgebra

Question

Let $(H,m,u,\Delta,\epsilon,S)$ be a Hopf algebra with product $m$, unit $u$, coproduct $\Delta$, counit $\epsilon$ and antipode $S$.

Coproduct of an element:

$$\Delta: H\to H\otimes H,\quad \Delta(h) = \sum h_{(1)}\otimes h_{(2)}$$

Q1 What is the meaning of the sum? Are we summing components of a basis for $H$?

---

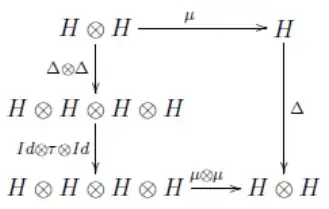
Also, we want $\Delta(m(h_{(1)}\otimes h_{(2)}))=(m\otimes m)((id\otimes \tau \otimes id)((\Delta \otimes \Delta) (h_{(1)}\otimes h_{(2)})))$

Which has:

$$RHS= (m\otimes m)((id\otimes \tau \otimes id)((\Delta \otimes \Delta) (h_{(1)}\otimes h_{(2)})))$$ $$= (m\otimes m)((id\otimes \tau \otimes id)(\sum h_{(1)(1)}\otimes h_{(1)(2)}\otimes h_{(2)(1)}\otimes h_{(2)(2)}))$$ $$= (m\otimes m)(\sum h_{(1)(1)}\otimes h_{(2)(1)}\otimes h_{(1)(2)}\otimes h_{(2)(2)})$$ $$=\sum h_{(1)(1)}h_{(2)(1)}\otimes h_{(1)(2)}h_{(2)(2)}$$

and $$LHS = \Delta( h_{(1)}h_{(2)})= \sum (h_{(1)}h_{(2)})_{(1)}\otimes (h_{(1)}h_{(2)})_{(2)}$$

So an axiom of the hopf algebra, says these are equal. But how does that make sense?

Answer 1

Regarding your first question: no we are not summing elements of any base. This is actually the Sweedler's notation for the comultiplication $\Delta: H\to H\otimes H$. What it does, is to suppress the explicit summation indices via the use of the abstract summation indices $_{(1)}$ and $_{(2)}$. So, instead of writting $\Delta(h) = \sum_{i,j=1}^{k} h_{i}\otimes h_{j}$ we use $\Delta(h) = \sum h_{(1)}\otimes h_{(2)}$. This is more abstract, but concrete enough to handle situations in which the conventional sigma notation would produce rather cumbersome expressions. For example, the comultiplication's defining condition is coassociativity i.e. $$(\Delta\circ Id)\circ\Delta=(Id\circ\Delta)\circ\Delta$$ If we apply Sweedler's notation, we get the following equivalent expression of coassociativity at the element's level: $$(\Delta\circ Id)\circ\Delta(h)=(\Delta\circ Id)(\sum h_{(1)}\otimes h_{(2)})=\sum \Delta(h_{(1)})\otimes h_{(2)}$$ and $$(Id\circ\Delta)\circ\Delta(h)=(\Delta\circ Id)(\sum h_{(1)}\otimes h_{(2)})=\sum h_{(1)}\otimes \Delta(h_{(2)})$$ thus, coassociativity means that for any element $h\in H$: $$\sum \Delta(h_{(1)})\otimes h_{(2)}=\sum h_{(1)}\otimes \Delta(h_{(2)})=h_{(1)}\otimes h_{(2)}\otimes h_{(3)}$$ (try expressing this using the usual tensor-like summation indices).

Now, regarding your second question, i guess you are actually talking about the relation: $$\Delta\circ m=(m\otimes m)\circ(Id\otimes \tau \otimes Id)\circ(\Delta \otimes \Delta)$$ which is the part of "compatibility" conditions between the algebraic and coalgebraic structure of $H$, in order for $H$ to be a bialgebra. Notice that both of the above maps (LHS and RHS) are of the form: $H\otimes H\rightarrow H\otimes H$. (see also the diagram below for a more detailed analysis of the maps). Let's compute the LHS: $$\Delta\circ m(g\otimes h)=\Delta(gh)=\sum (gh)_{(1)}\otimes (gh)_{(2)}$$ and the RHS: $$(m\otimes m)\circ(Id\otimes \tau \otimes Id)\circ(\Delta \otimes \Delta)(g\otimes h)= \\ (m\otimes m)\circ(Id\otimes \tau \otimes Id)\Big(\sum g_{(1)}\otimes g_{(2)}\otimes h_{(1)}\otimes h_{(2)}\Big)=(m\otimes m)\Big(\sum g_{(1)}\otimes h_{(1)}\otimes g_{(2)}\otimes h_{(2)}\Big)=\sum g_{(1)}h_{(1)}\otimes g_{(2)}h_{(2)}$$ so your condition (part of the definition of a bialgebra and a Hopf algebra) can now be equivalently written as: $$\Delta(gh)=\sum (gh)_{(1)}\otimes (gh)_{(2)}=\sum g_{(1)}h_{(1)}\otimes g_{(2)}h_{(2)}=\Delta(g)\Delta(h)$$ and actually says that: the comultiplication is an algebra homomorphism, between the algebras $H$ and $H\otimes H$ (equipped with its usual tensor product algebra structure).

An equivalent formulation of the above, is the commutativity of the following diagram: