How many rectangles can be observed in the grid?

Question

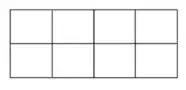
In a $2 × 4$ rectangle grid shown below, each cell is a rectangle. How many rectangles can be observed in the grid?

My attempt:

I found a formula somewhere,

Number of rectangles are $= m(m+1)n(n+1)/4 = 2\times4\times3\times5/4 = 30$.

Can you please explain this?

Upadte -

The post How many rectangles or triangles. looks similar, but that has $3 \times 4$ grid and I need more variant explanation.

This post should be reopened because this post has 12 times more views than linked post. — hululu, Aug 28 '18 at 07:29
See also: Analysis of how-many-squares and rectangles are are there on a chess board? — Martin Sleziak, Aug 28 '18 at 08:19
I asked here to reopen this post as some level of duplication is good: https://math.meta.stackexchange.com/a/29024/234055 — hululu, Aug 29 '18 at 11:59
@AkivaWeinberger, please see- https://math.meta.stackexchange.com/questions/28692/requests-for-reopen-undeletion-votes-volume-07-2018-today/29024#29024 — hululu, Sep 12 '18 at 14:09
@MithleshUpadhyay Having this many views and a negative score are, as far as I can tell, a great reason to delete. Getting that much attention and no positive feedback indicates it is not useful. I'm sure if you twittered one of the better-written duplicates, it would accrue at least as many views and a lot more upvotes (because their content is actually good.) . Anyhow, it doesn't give me any heartburn to have this question undeleted but closed as duplicate since so many links to more general problems have been provided. — rschwieb, Sep 12 '18 at 14:21
Ok sir, you vote for delete, but do you know who is Inventor of the Delete button;), that the guy is in the circle :). — hululu, Oct 01 '18 at 13:20

N. F. Taussig · Accepted Answer · 2016-02-15T13:35:09.707

4

To form a rectangle, we must choose two horizontal sides and two vertical sides. Since there are three horizontal lines, we can choose the horizontal sides in $\binom{3}{2}$ ways. Since there are five vertical lines, we can choose the vertical sides in $\binom{5}{2}$ ways. The number of rectangles we can form is $$\binom{3}{2}\binom{5}{2}$$

In general, the number of rectangles can be formed in a $m \times n$ rectangular grid with $m + 1$ horizontal lines and $n + 1$ vertical lines is the number of ways we can select two of the $m + 1$ horizontal lines and two of the $n + 1$ vertical lines to be the sides of the rectangle, which is $$\binom{m + 1}{2}\binom{n + 1}{2} = \frac{(m + 1)!}{(m - 1)!2!} \cdot \frac{(n + 1)!}{(n - 1)!2!} = \frac{(m + 1)m}{2} \cdot \frac{(n + 1)n}{2}$$

edited Feb 15 '16 at 13:35

answered Feb 15 '16 at 13:21

N. F. Taussig

79,074

Should we always assume a square to be a rectangle in such cases, if not mentioned otherwise? – kgkmeekg Apr 15 '16 at 04:55
Yes. A square is a rectangle in which adjacent sides are congruent. – N. F. Taussig Apr 15 '16 at 08:51
@N.F.Taussig, your answer is also going to delete :( – hululu Sep 11 '18 at 10:05
3

Duplicates are not automatically deleted. You could argue that the post should not be deleted since it has a useful answer. – N. F. Taussig Sep 11 '18 at 10:12

How many rectangles can be observed in the grid?

My attempt:

Upadte -

1 Answers1