36

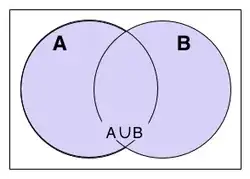
If $S = A \cup B$, then $S$ is the collection of all points in $A$ and $B$

enter image description here

What about $S = A \sqcup B$?, I think disjoint union is the same as union, only $A, B$ are disjoint. So the notation is a bit misleading. Because it is not a new operation, but operation where the pair $A,B$ satisfies $A \cap B = \varnothing$.

So given $A \cap B = \varnothing$, $S = A \sqcup B = A \cup B$.

Is my interpretation correct?

Your neighbor Todorovich
  • 8,472
  • 2
    In your picture, it looks like $A$ and $B$ are not disjoint. You can still attempt to write $A \sqcup B$ but it means you somehow alter $A$ and $B$ first to replace them with disjoint sets. But in some way that the new sets are "the same" as the old ones, for whatever purposes you have. – GEdgar Jan 29 '16 at 02:14

1 Answers1

54

The notation $A\sqcup B$ (and phrase "disjoint union") has (at least) two different meanings. The first is the meaning you suggest: a union that happens to be disjoint. That is, $A\sqcup B$ is identical to $A\cup B$, but you're only allowed to write $A\sqcup B$ if $A$ and $B$ are disjoint.

The second meaning is that $A\sqcup B$ is a union of sets that look like $A$ and $B$ but have been forced to be disjoint. There are many ways of defining this precisely; for instance, you could define $A\sqcup B= A\times\{0\}\cup B\times \{1\}$. This construction can also be described as the coproduct of $A$ and $B$ in the category of sets.

(This ambiguity is similar to the ambiguity between "internal" and "external" direct sums; see for instance my answer here.)

Community
  • 1
Eric Wofsey
  • 342,377
  • 11
    Well it seems the second meaning is used everywhere even on Wolframalpha, so I went crazy for a while until I decided to self medicate through mathstackexchange – Your neighbor Todorovich Jan 29 '16 at 02:15
  • 7
    In my experience, it is not common to actually write the notation $A\sqcup B$ for the first meaning, or to refer to "the disjoint union" (as opposed to just "the union") of $A$ and $B$ as a name for the union. Rather, you typically say something like "the set $X$ is the disjoint union of its subsets $A$ and $B$" when you already have a name $X$ for the union. – Eric Wofsey Jan 29 '16 at 02:23