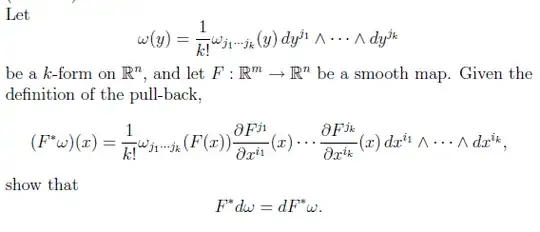The above question is from a past exam. I am having trouble with the fine details, ie what $F*dw$ and $dF*w$ actually look like. Can anybody show me how this question is solved? I have solved it using induction, but I don't believe this is what this question wants.
I will use the standard abuse of notation that is "multi-indices". We will write, for example
$$ \omega = \frac{1}{k!} \omega_{j_1...j_k} dy^{j_1} \wedge ... \wedge dy^{j_k} = \frac{1}{k!} \omega_J dy^J, $$
where $ J = ( j_1, ..., j_k ) $ is a "multi-index". Using this notation, your definition of pullbacks looks like
$$ F^* \omega = \frac{1}{k!} \left( \omega_I \frac{\partial F^I}{\partial x^J} \right) dx^J $$
so
\begin{align*} d F^* \omega &= \frac{1}{k!} \frac{\partial}{\partial x^i} \left( \omega_I \frac{\partial F^I}{\partial x^J} \right) dx^i \wedge dx^J \\ &= \frac{1}{k!} \left( \frac{\partial \omega_I}{\partial x^i} \frac{\partial F^I}{\partial x^J} + \omega_I \frac{\partial}{\partial x^i}\frac{\partial F^I}{\partial x^J} \right) dx^i \wedge dx^J. \end{align*}
The second term,
$$ \omega_I \frac{\partial}{\partial x^i} \frac{\partial F^I}{ \partial x^J} dx^i \wedge dx^J, $$
is equal to zero. Why? The multi-index is a product of terms so, more explicitly, what we want to show is
$$ \omega_{i_1...i_k} \frac{\partial}{\partial x^i} \left( \frac{\partial F^{i_1}}{ \partial x^{j_1}}... \frac{\partial F^{i_k}}{\partial x^{j_k}} \right) dx^i \wedge dx^{j_1} \wedge ... \wedge dx^{j_k} = 0. $$
First, note that if $i$ is equal to any of the $j$'s, the sum is zero because of the wedge products. Let's take an illustrative example of a non-zero term in the sum; let $i=2$ and $j_1=4$, the above has a term
$$ \omega_{i_1...i_k} \frac{\partial F^{i_1}}{\partial x^2 \partial x^{4}}... \frac{\partial F^{i_k}}{\partial x^{j_k}} dx^2 \wedge dx^{4} \wedge ... \wedge dx^{j_k}. $$
There is corresponding term where $i=4$ and $j_1=2$. This looks like
$$ \omega_{i_1...i_k} \frac{\partial F^{i_1}}{\partial x^4 \partial x^{2}}... \frac{\partial F^{i_k}}{\partial x^{j_k}} dx^4 \wedge dx^{2} \wedge ... \wedge dx^{j_k}, $$
which is the negative of the above term. Every term in the sum is either zero or cancels with a negative in this way (switching all the wedges around works since we need $k$ swaps to take $dx^k$ to the position of $dx^i$ and $k-1$ to get $dx^i$ to $dx^k$'s old position, making a total odd number of swaps). After concluding that the above is zero, we have
$$ d F^* \omega = \frac{1}{k!} \frac{\partial \omega_I}{\partial x^i} \frac{\partial F^I}{\partial x^J} dx^i \wedge dx^J. $$
Doing things the other way round, we get
$$ d \omega = \frac{1}{k!} \frac{ \partial \omega_I}{\partial y^i} dy^i \wedge dy^I $$
so
$$ F^*d\omega = \frac{1}{k!} \frac{ \partial \omega_I}{\partial y^i} \frac{\partial F^i}{\partial x^j} \frac{ \partial F^I }{ \partial x^J} dx^j \wedge dx^J = \frac{1}{k!} \frac{ \partial \omega_I}{\partial x^i} \frac{ \partial F^I }{ \partial x^J} dx^i \wedge dx^J, $$
where the last step follows by the chain rule. Hence, $ d F^* \omega = F^* d\omega $, as required.
