7

Placing 1x2 dominoes on an 8x8 chess board, in non-overlapping way, what is the lowest possible number of dominoes to lock (guard) the board, so that no further dominoes can be placed on the board? The aim here is to cover as little as possible and save the maximum number of unused dominoes

Thank you

RobPratt
  • 50,938
Manin
  • 101

1 Answers1

4

Regarding the original question, what is the lowest possible number of dominoes to lock the board (assuming that dominoes are actually $2\times1$, not $2\times2$):

The lowest possible number is 22. Here is an example of an optimal placing:

.11.22.3
44.55.63
.77.886.
99.AA.BB
.CC.DD.E
FF.GG.HE
.II.JJH.
KK.LL.MM

Regarding the question how to get this number:

I got that answer using dynamic programming (Python code).

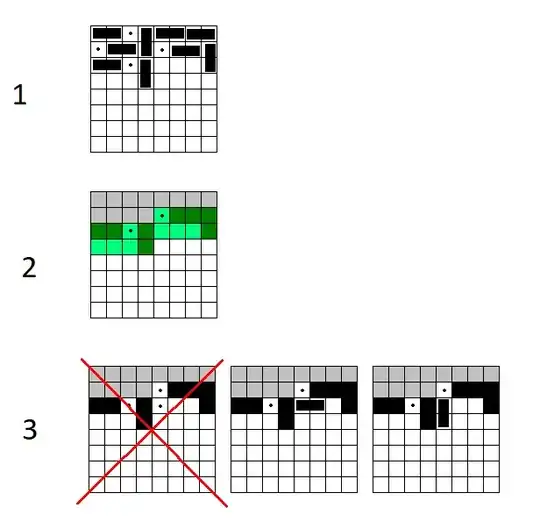
Suppose we have a board partly filled by dominoes and the "emptyness markers", see fig. 1 in the image below.

The generalized problem is: what is the lowest possible number of dominoes can be placed on the rest of the board to lock it? The answer depends only on the last two rows (green ones in fig. 2; note that it doesn't matter how occupied cells pair into dominoes, it only matters if the cell is occupied, or has an "emptyness marker" in it, or neither; and grey cells don't matter at all).

So, if we have seen the same two green rows before, we use the known result for this problem. Otherwise, we recursively try (fig. 3) to put an "emptyness marker" (impossible in this particular case because it would create two nearby empty cells), a horizontal domino, and a vertical domino in the first free cell (moving from top to bottom and from left to right in every row), and count the minimal number for these three cases; the result is stored in the cache.

Finally, we apply this method to the original problem when the board has nothing in it. The program checks all intermediate configurations and gives the answer. By the way, in this particular case of $8\times8$ board (perhaps in other cases, too) the optimal placing given above is the very first locking placing obtained by the sequential addition of the emptiness markers, the horizontal dominoes, and the vertical dominoes, as described above. So it could be obtained by simple greedy algorithm (but the optimality of that placing would require proof anyway, of course).

the explanative image

colt_browning
  • 3,647
  • It would be interesting to know more about your approach "using dynamic programming". How does this work? Note that the Question literally asks about placing $2\times 2$ dominoes on a board, but that seems to be a typo given the other figures in the Question and the OP's Comment. – hardmath May 30 '17 at 20:16
  • I have no doubt that "$2×2$ dominoes" is a typo. I did almost brute force search moving from left to right, from top to bottom of the board and recursively checking three options for every empty cell (leave empty, add a horizontal domino, add a vertical domino); and I used the important fact that if one of these three options have been picked for first $n$ rows then only rows No. $n$ and $n+1$ determine the possible placings in the rest of the board, so we can cache the result for the rest of the board and use it again when we get the same rows No. $n$ and $n+1$. I'll post the code tomorrow. – colt_browning May 30 '17 at 21:02
  • I'm not sure code would help Readers as much as a clear explanation of your search procedure. Dynamic programming suggests that you solve the stated problem by embedding it in a large family of problems to which recursion or another more explicit search procedure applies. – hardmath May 30 '17 at 21:42
  • 1
    @hardmath OK, once again. Suppose we have a board partly filled by dominoes and the "emptyness markers", see fig. 1 in the image. The subproblem you are talking about is: what is the lowest possible number of dominoes can be placed on the rest of the board to lock it? The answer depends only on the last two rows (green ones in fig. 2). So, if we have seen the same two green rows before, we use the known result for this subproblem. Otherwise, we recursively try (fig. 3) to put an "emptyness marker", a horizontal domino, and a vertical domino in the first free cell. – colt_browning May 31 '17 at 18:44
  • To the person who marked this answer for deletion: the question was "what is the lowest possible number of dominoes", not "how to find the lowest possible number of dominoes". I answered it precisely. – colt_browning May 31 '17 at 18:47
  • You've made an incisive observation in the Comment above, so I'd include it in the body of your Answer. Thanks. Comments are treated as "ephimeral" content. – hardmath May 31 '17 at 18:57
  • I've edited the answer to include all relevant information from the comments into it. Thanks for leading questions and tips. – colt_browning May 31 '17 at 19:51