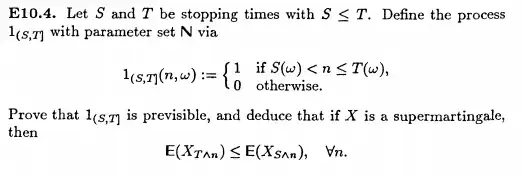Prove previsibility and $E[X_{T \wedge n}] \le E[X_{S \wedge n}]$

Question

From Probability with Martingales:

score 1 · Accepted Answer · edited Dec 15 '15 at 14:20

1

Show that $C_n:=1_{(S,T]}(n)$ is $\mathcal F_{n-1}$-measurable for each $n\ge 1$.
Use William's result 10.7(i), with the previsible process $(C_n)$ from 1 for a certain choice of stopping times.

(Last part is edited is by @BCLC. If John Dawkins doesn't rollback or edit, I'll assume e consents)

edited Dec 15 '15 at 14:20

BCLC

answered Dec 07 '15 at 22:24

John Dawkins

Thanks John Dawkins. Edited question to include attempt based on your answer. Not so sure about your #2 though. How about now? – BCLC Dec 08 '15 at 00:24
Added answer... – BCLC Dec 15 '15 at 14:39

score 0 · Answer 2 · edited Apr 13 '17 at 12:21

1.

B $ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ | \ \ \ $ preimage

$1 \in B,0 \in B$ | $\Omega$

$0 \notin B,1 \in B$ | $(S < n) \cap (T \ge n)$

$1 \notin B,0 \in B$ | $(S \ge n) \cap (T < n)$

$1 \notin B,0 \notin B$ | $\emptyset$

QED

Edit: Just to make explicit:

$$(S < n) \cap (T \ge n) = (S \le n-1) \cap (T \le n-1)^C$$

$$(S \ge n) \cap (T < n) = (T \le n-1) \cap (S \le n-1)^C$$

2.

$$S \le T$$

$$\to S \wedge n \le T \wedge n$$

$$E[\sum_{k=1}^{n}1_{(S \wedge n,T \wedge n]}(X_k - X_{k-1})] \le 0$$

$$\to E[\sum_{k=S \wedge n+1}^{T \wedge n}(X_k - X_{k-1})] \le 0$$

$$\to E[X_{T \wedge n} - X_{S \wedge n}] \le 0$$

$$\to E[X_{T \wedge n}] \le E[X_{S \wedge n}]$$

QED

2 Answers2