Why is $e$ the number that it is?

Question

Why is $e$ the number that it is? Most of the irrational number that we learn about in school have something to do with geometry, like $\pi$ is the ratio of a circle's diameter to its circumference. Those numbers can also be derived using maths ($\pi = \lim_{n\to\infty}4\sum_{k = 1}^{n}\frac{(-1)^{k+1}}{2k - 1}$). On the other hand, $e$ is derived only from math, and finds no other immediate geometric basis. Why then, is $e$ the number that it is ($2.7182\ldots$) and not some other number?

EDIT: My question is more along the lines of why $e$ is $2.7182\ldots$ On an alien world where there is a different system of numbers, could there be a similar constant that has all the properties of $e$, but is not $2.7182\ldots$?

The number $e$ has a lot of nice representations like the one you wrote for $\pi$, for example we have $e = \lim_{n \rightarrow \infty}\sum_{k=0}^n \frac{1}{k!}$. — 727, Dec 02 '15 at 18:57
In many ways, $e$ has a relationship to the unit hyperbola that is similar to the relationship $\pi$ has to the unit circle. — Brian Tung, Dec 02 '15 at 18:58
@KimPeekII: The summation to infinity typically is defined as the limit of the partial sums, is it not? — Brian Tung, Dec 02 '15 at 20:16
Perhaps, historically, it may have first arisen in connection to the area under a hyperbola. But I'm not sure. — Akiva Weinberger, Dec 02 '15 at 21:34
@AkivaWeinberger: The development of the natural logarithm (which of course has $e$ has its base) had its origin, I seem to recall, in the quadrature of the hyperbola. — Brian Tung, Dec 02 '15 at 22:02
Could you please add to your question: 1. How $e$ is defined for you; 2. What numbers you include in "Most...number(s)...in school have something to do with geometry"? Or are you "really" asking "How is $e$ defined?" — Andrew D. Hwang, Dec 03 '15 at 00:32
How $\sqrt{5}$ is connected with geometry in school? Just an example. — Integral, Dec 03 '15 at 00:37
@Integral Pentagons? 'Cause that's $2\phi-1$. (But then you'd ask about $\sqrt7$.) — Akiva Weinberger, Dec 03 '15 at 00:44
@AkivaWeinberger Yes, you know my point. They accept these irrational numbers but not $e$. Why? — Integral, Dec 03 '15 at 00:51
By the way, OP: In a very precise sense, the vast majority of real numbers are irrational. — Akiva Weinberger, Dec 03 '15 at 00:55
Here's something interesting. Recall that an open interval $(a,b)$ is the set of numbers between a and b exclusive. The length of an interval is defined to be $b-a$. Suppose I have a collection of open intervals ($I_1$, $I_2$, $I_3$, etc., to infinity) such that every rational number is contained in at least one of the intervals. (In symbols, $\Bbb Q\subset\bigcup_{n=1}^\infty I_n$.) What is the sum of the lengths of the intervals? Must it be infinity? Surprisingly, no! Turns out that it can be made as small as possible. I can have the lengths of the intervals add up to $0.01$, for example. — Akiva Weinberger, Dec 03 '15 at 01:04
(Cont'd) This is because the rationals are so rare in comparison to the irrationals. (We say that $\Bbb Q$ has measure zero, basically meaning that 0% of reals are rational.) — Akiva Weinberger, Dec 03 '15 at 01:08
Early in the development of logarithms, a base $1+x$ would be chosen with $x$ close to $0$, e.g. $x=0.000 000 1$ and, by repeated squaring, calculate approximate logs.That is $(1+x)^n\approx 2$ gives $\log x\approx 693147$ .The $\log$ would be "normalized" by multiplying by $x$. It was noticed that the same approximate number $2.718...$ would always come up as the one with normalized $log$ of $1$ regardless of $x$. — DanielWainfleet, Dec 03 '15 at 01:54
@AkivaWeinberger: I was talking about that (the Lebesgue measure of the rationals) yesterday, and I remarked that although I find the countability of the rationals straightforward to internalize (because I can visualize a list of the rationals that I know will contain all of them), I find the notion of a countable collection of intervals containing every rational in $[0, 1]$ that have a combined length of less than $1$ weird in the sense that I can't really visualize it. I can construct it, but visualization beyond the coarse appearance of it escapes me. — Brian Tung, Dec 03 '15 at 17:27
@Integral: Although, as Akiva Weinberger points out, we can relate $\sqrt{5}$ to pentagons, we can also merely construct it as the hypotenuse of a right triangle whose legs have lengths $1$ and $2$. In other words, it is a constructable number, as is $\sqrt{7}$, which does not have an obvious interpretation in any common figure. It can, however, be constructed as a the hypotenuse of a right triangle whose leg lengths are $\sqrt{5}$ (constructed as before) and $\sqrt{2}$, which is in turn the hypotenuse of a isosceles right triangle with leg length $1$. This may seem contrived, but $e$... — Brian Tung, Dec 03 '15 at 17:40
@Integral (cont'd): ...and $\pi$ (and in fact most irrational numbers) are different in that they cannot be constructed (using a straightedge and compass). That they have geometrical interpretations (when in fact they do) is an accident of their being defined in a particular way. — Brian Tung, Dec 03 '15 at 17:41
Just like $\pi$ can be obtained by simulation using e.g. Buffon's needle, $e$ is the expectation of the number of uniforms one needs to add to exceed $1$, as well as the average number of uniforms one must draw to see a break of the monotonicity of the sequence. — Xi'an ні війні, Apr 26 '16 at 19:50
This is one of the best questions posted here and should be re-opened. If I could post an answer I would mention the following. It is easy to show that $(d/dx) 2^x = (2^x\cdot\text{constant}) \approx 2^x\cdot 0.69$, or $(d/dx) 10^x = (10^x\cdot\text{constant}) \approx 10^x \cdot 2.3.$ It is only when the base is $e$ that the constant is $1$, thus: $(d/dx) e^x = (e^x \cdot\text{constant}) = e^x\cdot 1.$ This is similar to the reason why radians are used in calculus: $(d/dx) \sin x = (\text{constant}\cdot\cos x),$ and the "constant" is $1$ only if radians are used. $\qquad$ — Michael Hardy, Jul 31 '16 at 07:08
Related question: http://math.stackexchange.com/questions/26037/intuitive-understanding-of-the-constant-e/ — Gerry Myerson, Jul 31 '16 at 09:22

Brian Tung · Accepted Answer · 2015-12-03T00:39:00.917

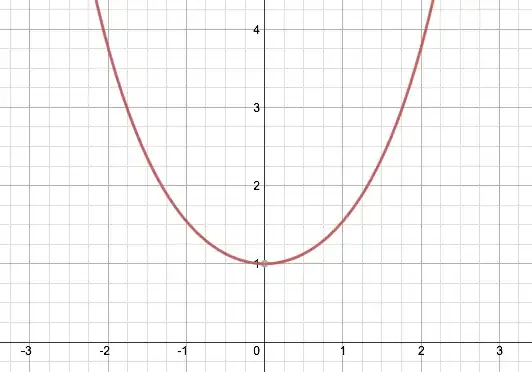
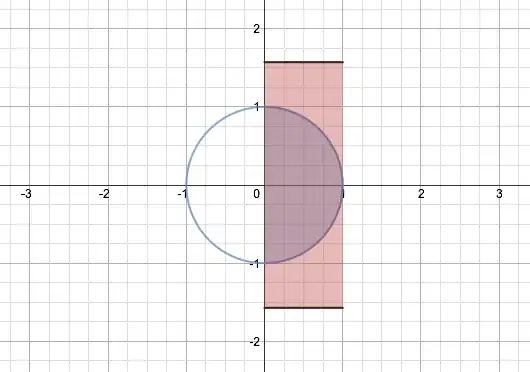
Let's begin with a geometric interpretation that is, admittedly, a little contrived, but may give some satisfaction. Consider a circle, and construct a rectangle whose width is one of the circle's radii. If we extend the black lines outward until the two orange areas together have the same area as the purple semicircle, the length of the rectangle is $\pi$ times its width:

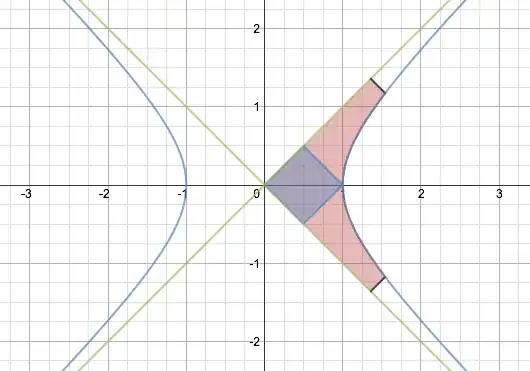
Next, consider a right hyperbola (that is, one in which the asymptotes are at right angles). If we extend the black lines outward until each of the orange areas individually have the same area as the purple square, those black lines are each $e$ times as far out from the center as the side of the square:

Now, some other observations:

Remember that hyperbolic sine and cosine are defined as

$$ \cosh\phi = \frac{e^\phi+e^{-\phi}}{2} $$ $$ \sinh\phi = \frac{e^\phi-e^{-\phi}}{2} $$

so that $e$ is as important to these functions as $\pi$ is to ordinary sine and cosine.

The unit circle $x^2+y^2 = 1$ can be parametrized as $(\cos\theta, \sin\theta)$, and then the area of the sector subtended at the center by the circle, from $0$ to $\theta$, is $\theta/2$. Similarly, the unit hyperbola $x^2-y^2 = 1$ can be parametrized as $(\cosh\phi, \sinh\phi)$, and then the area of the sector subtended at the center by the hyperbola, from $0$ to $\phi$, is $\phi/2$.

Equivalently, just as we have $\cos^2\theta+\sin^2\theta = 1$, we have $\cosh^2\phi-\sinh^2\phi = 1$.

The figure produced by a hanging chain of uniform density is called a catenary (from Latin catena "chain"), and is simply $y = \cosh x$:

An excellent answer! +1. This is a very beautiful construction that I've been trying to find — Yuriy S, Mar 02 '16 at 17:17

score 8 · Answer 2 · answered Dec 02 '15 at 18:55

8

The significance of $e$ is that it is the only number satisfying $\frac{d}{dx}e^x=e^x$.

answered Dec 02 '15 at 18:55

parsiad

25,738

score 8 · Answer 3 · answered Dec 02 '15 at 21:22

8

$$e^x\ge x+1,\quad\text{for all }x$$ This uniquely defines $e$, and is my personal favorite property of $e$. (This is partly because it defines it without appealing to calculus.)

Basically, if you want to do inequalities with exponentials, you need $e$. (For example, what is the smallest value of $x^x$? The answer is $(\frac1e)^{1/e}$, at $x=\frac1e$.) A similar thing happens with trig functions and radians.

answered Dec 02 '15 at 21:22

Akiva Weinberger

25,412

3

I agree on the favorite property. I myself often try to answer e-related questions here solely from $\exp(x)\ge 1+x$ and $\exp(x+y)=\exp(x)\exp(y)$. – Hagen von Eitzen Dec 02 '15 at 21:38
1

A while ago I figured out how to prove that:$$\ln2=1-\frac12+\frac13-\frac14+\dotsb$$just using those (and the squeeze theorem at the very end), without calculus. However, I haven't figured out how to do the same with $\ln2=\sum_{n=1}^\infty\frac1{n2^n}$. – Akiva Weinberger Dec 02 '15 at 21:49
It is a bit illusory to say that this defines $e$… if you wish to prove the existence of a unique number $e$ that satisfies this property, calculus is all over the proof. But I like this nonetheless. – Lee Mosher Dec 03 '15 at 02:15
@LeeMosher Well, not really. Pretty sure you just need Cauchy's intersection theorem, or maybe even just the squeeze theorem. A bit analysis-y, but not really "calculus all over it." – Akiva Weinberger Dec 03 '15 at 02:22

score 3 · Answer 4 · edited Dec 02 '15 at 19:28

The definition of $e$ is as follows: $$\lim_\limits{n\to \infty}\left(1+\frac{1}{n}\right)^n=e$$ and hence $$2<e<3$$

Apart from that, $e$ has other representations as well: $$e=\sum_{n=0}^\infty \frac{1}{n!}$$

And from the point of view of geometry, consider Euler's famous formula: $$e^{i\theta}=\cos \theta+i\sin \theta$$

This has immense importance in geometry of complex numbers, especially in case of "rotation".

score 3 · Answer 5 · answered Dec 02 '15 at 18:57

$e$ has a highly geometrical interpretation when you consider $e^{i \theta}$: it becomes a description of the idea of "rotation".

Additionally, $e$ occurs physically in a very wide range of situations: any time growth compounds with itself to cause further growth, there will be an exponential lurking beneath the surface. $e$ turns up in the real world all the time.

Mirko · Answer 6 · 2015-12-02T21:16:13.020

If you consider the functions $a^x$, where $0<a<1$ or $a>1$, all these functions have the point $(0,1)$ on the graph (this is the only point common to all these graphs, so it is obviously an important point).

Only for $e^x$ does this function have slope exactly $1$ at $(0,1)$. The number $1$ is important as it is the so called multiplicative identity, $x\cdot 1=x$ for all $x$. So $e$ is important as being the specific base that makes $e^x$ the only function, among all $a^x$, that has slope $1$ at the point $(0,1)$. Slope $1$ is also geometrically significant as the only slope for which "rise"$=$"run".

This Play Name · Answer 7 · 2015-12-02T21:26:22.283

2

I don't think there is one set reason as to "why" $e$ is what it is. $e$ is a number that satisfies many properties, much like $\pi$ and that is in a way $e$ is the number that it is. Along with the fine properties that the other answers have provided I'll include one of the first things Euler discovered about $e$ was the continued fraction: $e = 2+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1+ \cfrac{1}{1 + \cfrac{1}{4 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{6 + \cdots}}}}}}}}$
Notice the pattern or even numbers. I find that to be extremely interesting about $e$.

edited Dec 02 '15 at 21:26

answered Dec 02 '15 at 21:13

This Play Name

668

4

Douglas Hofstadter pointed out in his book Fluid Concepts and Creative Analogies that the initial $2$ doesn't fit the nice repeating $[\ldots, 1, 2n, 1, \ldots]$ pattern, but that blemish goes away if you reinterpret the continued fraction as $[1, 0, 1, 1, 2, 1, 1, 4, 1, 1, 6, 1, \ldots]$ instead. – Dec 03 '15 at 00:26

score 1 · Answer 8 · answered Dec 02 '15 at 18:58

1

The identity (which can be seen as a definition) $e^{i\theta} = \cos\theta + i\sin \theta$ is geometrically significant. If you delve into the subject of complex analysis, you'll understand that $e^{i\theta}$ can be seen as a "rotation".

answered Dec 02 '15 at 18:58

GiantTortoise1729

3,098

score 1 · Answer 9 · answered Dec 02 '15 at 19:16

Not forget to mention:

$$e^x = \sinh(x) + \cosh(x)$$
$e$ is fundamental for the Theory of Representations in Group Theory, essential topic in Quantum field theory, quantum mechanics and particle physics
$e$ arises also from the "compound interests" problem in economics
It's fundamental for Fourier transforms, Stirling approximation and Gaussian curves (so that it's fundamental in Data Analysis and Probability and Statistics)

score 1 · Answer 10 · answered Dec 02 '15 at 21:23

1

$e$ is like matrices. Or sets. When you first learn them, you think, "Err...so what?" As you learn more mathematics, you find yourself using these things more and more, until you can't imagine doing mathematics without them.

answered Dec 02 '15 at 21:23

TonyK

68,059

score 0 · Answer 11 · answered Dec 03 '15 at 02:06

For $u>0$ and $f(u)=\int_1^u (1/x)dx$ , a geometric representation of $e$ is that $f(e)=1$. The region bounded by the $x-$axis, the line $y=1$,the graph of $y=f(x)$, and the line $y=u$, has area $1$ when $u=e$. This can be taken as a definition of $e$, analogous to the definition of $\pi$ as the area of a semi-circle of radius $1$.

Why is $e$ the number that it is?

11 Answers11

Linked