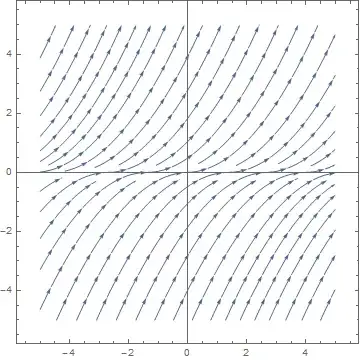
While trying to solve the differential equation: $y'=\sqrt{|y|}$. I got confused how to deal with the absolute value. I want to draw a sketch for the direction field for that equation, and see for what initial values does this equation fulfill the conditions of the existence and uniqueness Theorem.
I tried to do the integral according to the sign, depends if $(y>0)$ or $(y<0)$. but I'm still not sure if my result is right.
result that I got:
- while $y>0$ : $y=({\frac{x}{2}+c})^{2}$
- while $y<0$ : $y=({-\frac{x}{2}+c})^{2}$
if that's the case, Its hard for me to imagine the Direction field by these two equations, because they are always above axis: $x$. How does it look? any hints?