Let’s start by clarifying things: you have two situations summarized by the following drawings
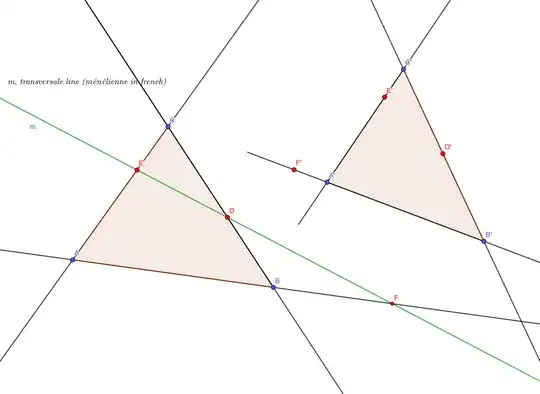
So, the situation is :
1.- We have $ABC$ and $E\in AC, D\in CB$ and $F\in AB$
It is important to understand that the points are considered anywhere on the lines that support the segments which are the sides of the triangle(see for example $F$: $F\notin [AB], F\in AB$ on the figure)
2.- Then, Menelaus’ theorem establishes a link between the fact that D, E, and F are aligned and “complicated” ratios.
We can now state this theorem, which is an equivalence, by trying to simplify the “complicated” ratios through the use of colors.
Theorem: $\color{red}{E,D, F}$ are $\color{darkgreen}{\text{aligned}}$ if and only if $$\frac{\overline{A...}}{\overline{B...}}\frac{\overline{B...}}{\overline{C...}}\frac{\overline{C...}}{\overline{A...}}=1$$
Let’s fill in the gaps now
$$\frac{\overline{A\color{red}{F}}}{\overline{B\color{red}{F}}}\frac{\overline{B...}}{\overline{C...}}\frac{\overline{C...}}{\overline{A...}}=1$$
Note that $\color{red}{F}\in AB$
$$\frac{\overline{A\color{red}{F}}}{\overline{B\color{red}{F}}}\frac{\overline{B\color{red}{D}}}{\overline{C\color{red}{D}}}\frac{\overline{C\color{red}{E}}}{\overline{A\color{red}{E}}}=1$$
You would have normally guessed why to place D like this and E like that.
Finally, your questions boil down to:
1.- what is the algebraic value $\overline{MN}$?
2.- And why does this come into play here?
3.- Which is the correct one and why is the other wrong?
4.- If both are correct,how are both correct?
1.- Take any line $l$. Choose an origin $0$ on it and another point $I$ different from $0$ on it. Then there is a well known bijection between $l$ and $\mathbb R$, once you have chosen $0I$ as unit of length and decided that $I=1$. It’s an abuse of notation since a point is obviously not a real number, but it’s an abuse of notation that everyone does, you too I hope : If I ask you to place point A=4 or point B=-7 or point C=-2, you will place them without much hesitation, accepting these abuses of notation without difficulty. We give a scholarly name to these identifications and talk about isomorphism, here a non-canonical isomorphism of vector spaces but it doesn’t matter: a primary school student does it without needing all these mathematics. When he has grown a little, he learns to calculate $\vec{CB}=B-C=-7-(-2)=-7+2=-5$. That is what we note $\overline{CB}=-5$. And we have $$CB:=|\overline{CB}|=|-5|=5$$
2.- As always in mathematics, we really understand theorems only when we are able to prove them. The demonstrations proposed by Wikipedia are not mine, where I use more advanced notions (projective completion of an affine plane, homogeneous coordinates, determinant of order 3, … all the mathematical apparatus at my disposal to demonstrate in a few lines the theorem of Menelaus). So I’m not going to give this complete demonstration here, but just the beginning that uses precisely $$\overline{MN}$$ for $M,N \in $ an affine plane.
So, at the beginning of that proof, we begin by writing $$\overline{DC}.\overline{DB}-\overline{DB}.\overline{DC}=0$$
what is reasonable, isn’t it?
Then, we need to translate that into $$\overline{DC}.\overrightarrow{DB}-\overline{DB}.\overrightarrow{DC}=\vec0$$
Then $\vec{DB}=\frac {\overline{DB}}{\overline{DC}}\vec{DC}$ And $$\frac {\overline{DB}}{\overline{DC}}$$ $$=\frac{\overline{B\color{red}{D}}}{\overline{C\color{red}{D}}}$$appears naturally.
And the demonstration then ends in 3/4 lines provided that the powerful tools mentioned above are used.
That’s why it comes into play in that demonstration.
3.- The first one (1) is then correct if it is considered with algebraic values (use $\overline{MN}=-\overline{NM}$) and obviously FALSE if it is considered without algebraic values. The second one (2) is TRUE if it is without algebraic values and FALSE if it is considered with algebraic values
4.- Both are then correct in a certain sense:(1) with algebraic values and (2) without.
The best way in mathematics to appropriate knowledge is always to look at examples. Here is one
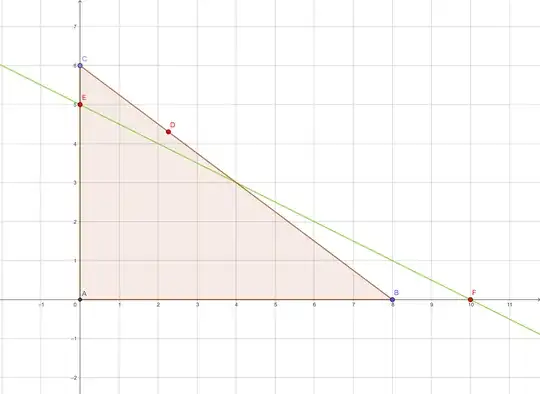
In $\mathbb C, A=0,B=8,C=6i, E=5i, F=10$
According to Menelaus theorem,
$E, D, F $ are aligned iff $\frac{\overline{A\color{red}{F}}}{\overline{B\color{red}{F}}}\frac{\overline{B\color{red}{D}}}{\overline{C\color{red}{D}}}\frac{\overline{C\color{red}{E}}}{\overline{A\color{red}{E}}}=1$
$$\iff \frac{\overline{B\color{red}{D}}}{\overline{C\color{red}{D}}}=\frac{\overline{B\color{red}{F}}}{A\overline{\color{red}{F}}}\frac{A\overline{\color{red}{E}}}{\overline{C\color{red}{E}}}$$
I’ll let you try to conclude, hoping that my explanations help you do so.

