Equilateral polygon plane tiling

Question

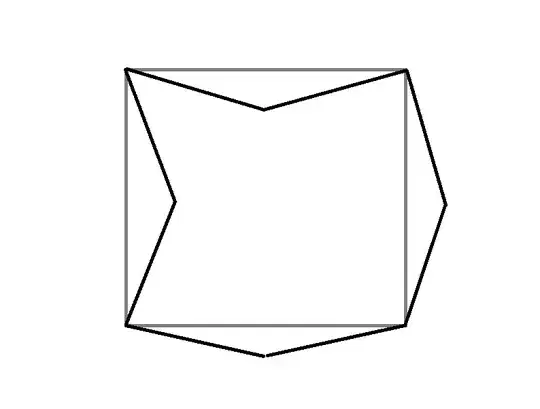
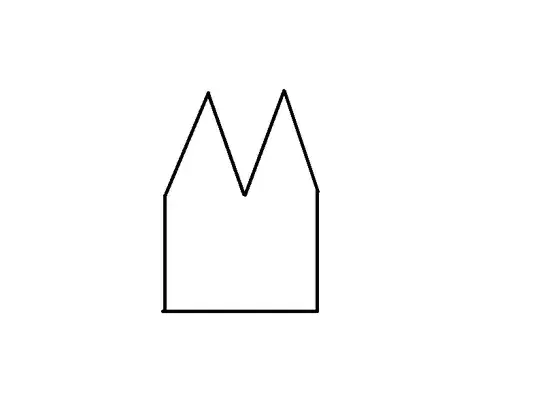
From playing around with some toothpicks and peas, I think that it should be possible to prove that the plane cannot be tiled by a possibly infinite set of equilateral polygons with the same number of sides whenever $n>6$, though I am not sure regarding $n=5$.

Is there a simple proof / contradiction to the above?

When $n$ is too large, you can calculate the angles and see that the polygons can't fit around a single point. You could also use the Euler characteristic on a finite (but large) tiling. — Michael Burr, Nov 12 '15 at 21:15
@michaelBurr: Hence the claim. The generalization to $n$ got a bit messy though. — Nathaniel Bubis, Nov 12 '15 at 21:18
As Dan Rust's answer shows, the claim is false for equilateral polygons, but it is true for regular polygons (which have equal angles in addition to equal sides). — Brian Tung, Nov 13 '15 at 08:02

score 6 · Accepted Answer · edited Nov 13 '15 at 08:09

6

Just crinkle the edges of a square. This will at least let you form an equilateral $2n$-gon for any $n\geq 2$.

For $n$ an odd numbers of edges just have a church with $(n-3)/2$ `steeples'.

You can clearly tile the plane with such shapes.

edited Nov 13 '15 at 08:09

Nathaniel Bubis

33,425

answered Nov 13 '15 at 00:55

Dan Rust

30,973

I don't see how that proves anything about whether or not you can tile the plane. – Nathaniel Bubis Nov 13 '15 at 07:53
2

@nbubis: ??? Just take the first diagram and fill the plane with it. – Brian Tung Nov 13 '15 at 08:00
1

For the second diagram, line them up side by side, and then construct an identical line, but upside down. These sawtooths will meet and create a single straight stripe. This allows you to tile the plane as well. – Brian Tung Nov 13 '15 at 08:01
Slow morning :) Thank you! – Nathaniel Bubis Nov 13 '15 at 08:10

Equilateral polygon plane tiling

1 Answers1

Linked