Runge-Kutta methods: step size greater than 1

Question

The local truncation error of Runge-Kutta 4 is $O(h^5)$, while those of RK1 is $O(h^2)$.

I wonder then what happened when the step-size of RK methods is greater than 1: will the accuracy be improved if we choose RK1 instead of RK4?

Answer 1

The $\epsilon = O(h^p)$ describes behavior of the error when $h$ tends to zero. You cannot compare $O(h^2)$ and $O(h^5)$ just simply by comparing $h^2$ and $h^5$, in fact they have different multipliers, $$ \epsilon_\text{Euler} \approx C_E h^2\\ \epsilon_\text{RK4} \approx C_{RK4} h^5 $$ where both $C_E$ and $C_{RK}$ depend on the problem being solved.

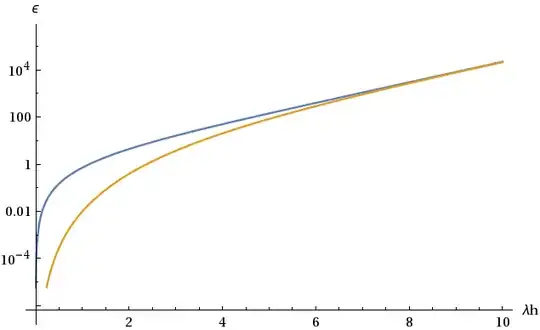
For example, when these methods are applied to a linear ODE $$ u' = \lambda u\\ u(0) = 1 $$ the local truncation error is $$ \epsilon_n = u_n \left[e^{\lambda h} - r(\lambda h)\right], $$ where $r(z)$ is so-called stability function of the method. For the explicit Euler the stability function is $$ r_E(z) = 1 + z $$ and for the RK4 it is $$ r_{RK4} = 1 + z + \frac{z^2}{2} + \frac{z^3}{6} + \frac{z^4}{24}, $$ so $$ \epsilon_{E} = u_n \sum_{k = 2}^\infty \frac{\lambda^k h^k}{k!}\\ \epsilon_{RK4} = u_n \sum_{k = 5}^\infty \frac{\lambda^k h^k}{k!}. $$ It can be seen that it is not $h$, but $\lambda h$ what the ocal truncation error depends on. For systems of ODE the role of $\lambda$ roughly play the eigenvalues of the jacobian matrix of the system.

Here are $\epsilon_{E}$(blue) and $\epsilon_{RK4}$(yellow) plotted against $z = \lambda h$. The errors are almost the same (and really big) for moderate values of $z \gtrsim 5$. Both error behave like $\epsilon \approx e^z$ for big $z$, so the relative error is about $1$.