The original question is Baby Rudin's problem 6.13(c), where I am asked to compute the upper and lower limits for $$\frac12(\cos(x^2)-\cos((x+1)^2))+\mathcal O(\frac1x)$$ as $x\to+\infty$.
The question is equivalent to the one asked in the title.
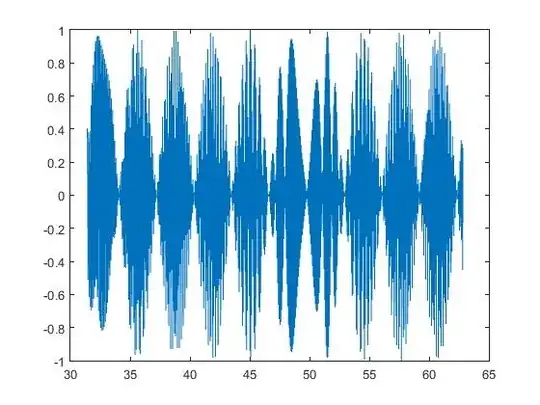
From a graphical point of view (as is shown below, with $x$ ranging from $20\pi$ to $30\pi$), the answers are clearly $1$ and $-1$.
But how on earth am I supposed to construct a fitting sequence $x_n$? When I was trying to obtain the upper limit I tried the form $$x_n=\frac12 \pi-\frac12+2k_n\pi$$ with two conditions $$k_n\to 0 \mod 1\quad\text{and}\quad x_n^2\to0\mod 2\pi $$ but it was so hard to find a proper $k_n$ that I had to give up.
I really need some help here. I'd be grateful if you would enlighten me. Thanks in advance.