42

This problem occurred to me when I came across a similar problem where the radii were taken over only the primes. That question was unanswered, but it seems to me infinitely many circles of radius $1/2, 1/3, 1/4...$ can fit into a unit disk. The area of all those circles would be $\pi \sum_2^\infty 1/n^2 = \pi^3/6 -\pi$, which is less than the area of the unit disk $\pi$. But can the circles actually be packed with no overlaps?

Martin Sleziak
  • 56,060
Rob
  • 7,520
  • 1
    See Descartes' theorem. – Lucian Oct 22 '15 at 08:26
  • 2
    Consider the Apollonian gasket generating by packing two circles of radius $1/2$ and two circles of radius $1/3$ into a circle of radius $1$. I have a feeling that all the circles of radius $1/n$ can fit into the circle of radius $1$ while touching it as well. – eyqs Oct 24 '15 at 04:33
  • I've been thinking about this problem, and I think it could be proved if one could generate a function that gives the radius of the biggest possible circle that can fit, given that circles of radius $1/2, 1/3, 1/4...1/n$ have already been packed into it, and prove that that function is always greater than $1/(n+1)$. For example, if the unit disk has a circle of radius $1/2$ already in it, the maximum possible circle that can still fit is another circle of radius $1/2$, and the same for the unit disk packed with two circles $1/2$ and $1/3$, but I don't know about $1/4$ – Rob Oct 24 '15 at 20:27
  • 2
    I mean it's totally believable that this can be done. The sum of the areas of the circles you want to pack is roughly $2,02$ and the unit disk has area $3,14$ roughly. This leaves roughly $1,12$ units of area and after placing the first few circles, the radius get smaller and smaller ; fitting them within $1,12$ units of area, no matter how the first $N$ circles are positioned, should be absolutely no problem. It's as if you were asking if it were possible to fit a pingpong ball, a pea and sand in a bottle. Just throw them all in. It'd be hard to give you a very "sweet" pattern though. – Patrick Da Silva Oct 26 '15 at 23:30

3 Answers3

41

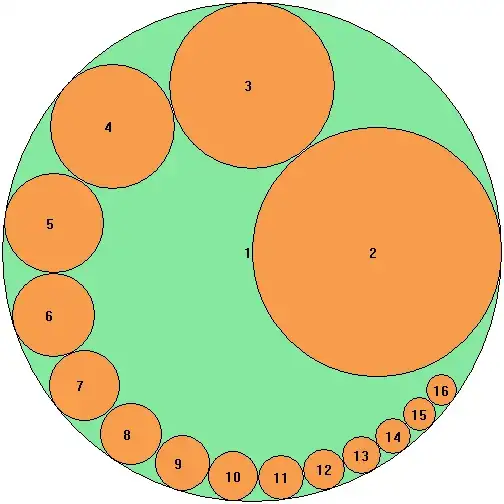
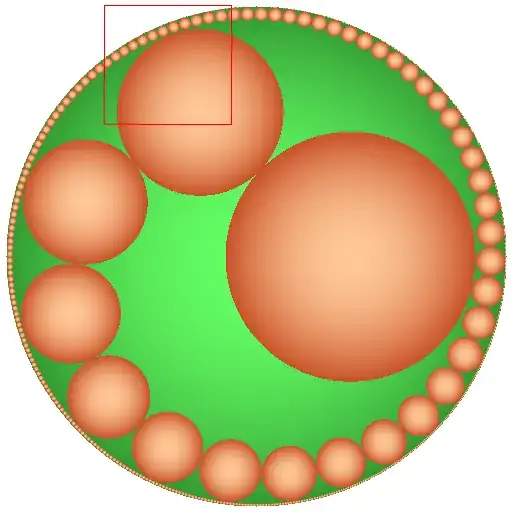
This packing of first circles with radii $\dfrac{1}{2}, \ldots, \dfrac{1}{16}$ gives me optimism in possibility of such packing:

enter image description here

Next step: one can cut free room into strips, which can be packed with smaller circles...
Sketch is below:

enter image description here

$2$nd strip: circles with radii $\dfrac{1}{17}, \ldots, \dfrac{1}{47}$; $3$rd strip: circles with radii $\dfrac{1}{48},\ldots,\dfrac{1}{99}$ (for example).

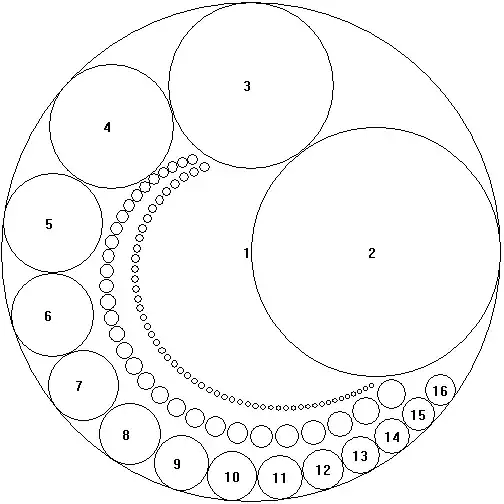
Update: And this packing is, maybe, more elegant:

enter image description here

One note: when arrange circles in row, then "tail" is fast-convergent: enter image description here

while radius is $\dfrac{1}{n}$, then $y = \dfrac{2}{n}$, $x = 2\sum\limits_{k=1}^n \dfrac{1}{n} \approx 2(\ln n +\gamma)$, where $\gamma \approx 0.577$; therefore red line has formula $y = 2 e^{\gamma}e^{-x/2}$. In the previous image this "tail" is rolling infinite number of times near the main circle, but its width is very-very tiny. Each loop is $\approx e^{\pi}\approx 23.14$ times thinner than previous one. So total thickness of tail (starting of $n$-th circle) has the same behavior: $\tilde ~ e^{-1/(2n)}$.

Oleg567
  • 17,740
  • Here is an simple idea which may be of some use. Suppose you want to fit in the circles of radii $1/n$ for $n = 2^k,2^{k}+1, \dots, 2^{k+1}-1$. You can then pile them one on top of the other into one rectangle with sides $1/2^{k-1}$ and $2$, or $1/2^k$ and $1$, etc. Repeating this construction, you can fit all the circles with $n \geq 2^k$ into a rectangle $1/2^{k-1} \times 1$. Your picture almost goes up to at least $n = 64$. Can you fit a rectangle $1/32 \times 1$ in the unoccupied are? – Jakub Konieczny Oct 26 '15 at 16:31
  • 1
    @Feanor, yes, on the 1st image there is such free space for $1/32\times 1$ rectangle, when circles $17, ..., 99$ move away to free gaps (like right-top corner etc.). I tried recently to draw image in "one style", arranging circles along circumference. – Oleg567 Oct 26 '15 at 23:23
25

Consider lining up all circles with radii $1/2...1/n$ such that each circle is tangent to the two circles next to it, and all the circles are tangent to a straight line. The function which approximates their heights as $n\rightarrow\infty$ is $\sqrt{e^{-n}}$, as shown below

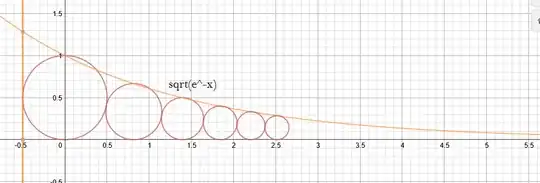enter image description here $\int_{-1/2}^{\infty} \sqrt{e^{-n}}dn = 2\sqrt[4]{e}$ ~$2.568... \lt \pi$, therefore the whole function can be contained inside the unit circle as a beautiful spiral, $r=1-\sqrt{e^{-\theta}}$ 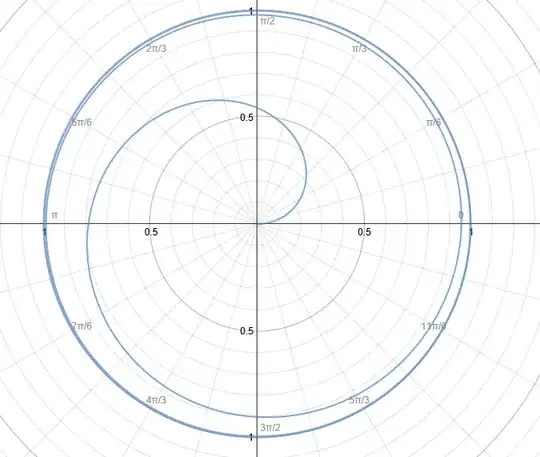enter image description here This perfectly matches @Oleg567's elegant packing.
Rob
  • 7,520
16

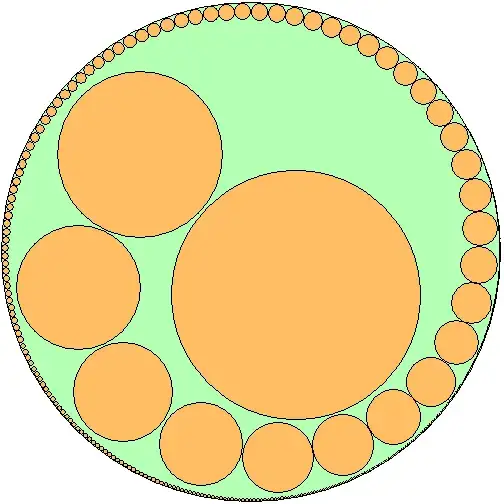
Just to make geometry more attractive:
(on "pingpong ball, a pea and sand in a bottle"... see comment of @Patrick Da Silva :)
Inscribed circles

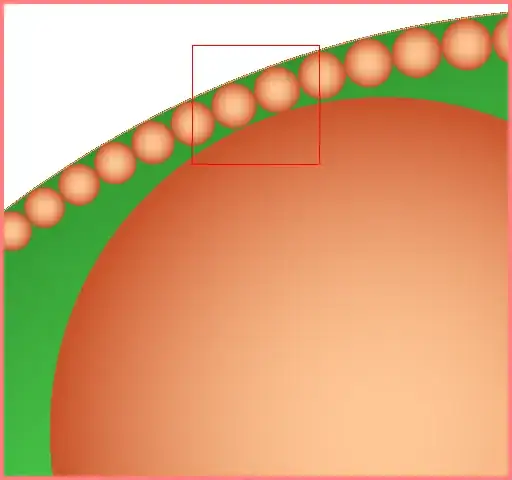
$4\times$ scaled left-top corner:
Inscribed circles (4x)

$4\times$ scaled left-top corner of $2$nd image:
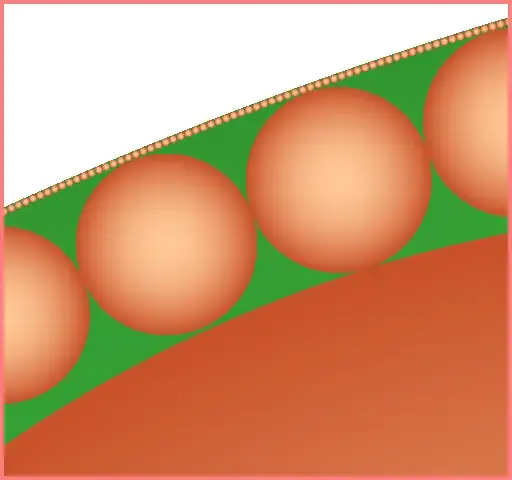
Inscribed circles (16x)

One can see fractal property of these images.

Oleg567
  • 17,740