10

Dynamic programming usually works "backward" - start from the end, and arrive at the start. This works both when there is and when there isn't uncertainty in the problem (e.g. some noise in the state). The backward DP algorithm is then (for the case of no noise):

enter image description here

Initialization: $$J_N(i)=a_{iT}^N\quad i\in S_N$$

Iteration: $$J_k(i)=\min_{j\in S_{k+1}}\left( a_{ij}^k+J_{k+1}(j) \right)\quad i\in S_k,\quad k=N-1,N-2,...,0$$

For deterministic (no uncertainty) problems, we can reverse the algorithm and say that we can do the same thing starting from the start and ending at the end, and that the solution will be the same - this is forward DP. By transforming the above-written backward DPA, we obtain the forward DP algorithm (by flipping the arrow directions in the above figure):

Initialization: $$\tilde J_N(j)=a_{sj}^0\quad j\in S_1$$

Iteration: $$\tilde J_k(j)=\min_{i\in S_{N-k}}\left( a_{ij}^{N-k}+\tilde J_{k+1}(i) \right)\quad j\in S_{N-k+1},\quad k=N-1,N-2,...,0$$

However, I don't understand why the above cannot be applied also to stochastic problems, i.e. Thank you for your help!

space_voyager
  • 1,205
  • 2
    In both the deterministic and stochastic cases: The backward algorithm has the interpretation that the cost function at each state is the cheapest remaining (expected) cost to get to the destination starting from that state.

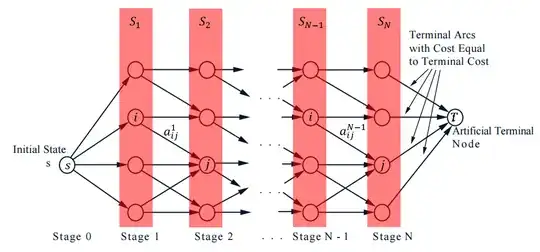
    In the deterministic case: The forward algorithm has the interpretation that the cost function at each state is the cheapest way to get to that state (starting from the beginning). However, in the stochastic case, how do we make sure we really get to that state (given the state transitions are random)?

     – Michael Oct 17 '15 at 15:18
  • So, if only the costs were random (rather than the state transitions), we could indeed apply the forward algorithm for stochastic problems. However, why do we care about doing a forward algorithm when we can always do a backward algorithm? – Michael Oct 17 '15 at 15:23
  • @Michael I think, intuitively, I understand thanks to your comment. But I'd appreciate an example where, by trying to do forward DP on a stochastic problem, we truly get stuck - as in a point comes where something mathematical blocks us from going further. Would you be able to provide such an example in an answer? I'd really appreciate it. – space_voyager Oct 17 '15 at 15:28
  • Well, why not design your own example and try it out? – Michael Oct 17 '15 at 15:29
  • 1
    @Michael I tried, believe me. I'm new to dynamic programming, which is why I posted here hoping someone more at-ease with the concepts can provide an example that'll make my thinking click, and then I'd be able to think of my own further examples. – space_voyager Oct 17 '15 at 15:30

0 Answers0