2

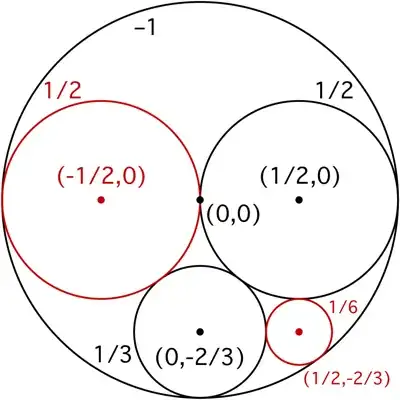
Given two points inside the unit circle, $(x_1, y_1)$ and $(x_2, y_2)$, let $C_1$ and $C_2$ be the circles with centers at those points, respectively, which are internally tangent to the unit circle. If $C_1$ and $C_2$ are externally tangent to each other, how can I find the center $(x, y)$ of the circle $C$ which is internally tangent to the unit circle and externally tangent to both $C_1$ and $C_2$?

I know that the radii of the circles will satisfy the Descartes Circles Theorem, and that the unit circle must be the external Soddy Circle for $C$, $C_1$, and $C_2$, so I could theoretically back-solve for $(x,y)$ knowing that $(0,0)$ is the isoperimetric point of the triangle with vertices at each circle's center, but that could get real ugly real quick.

If $C$, $C_1$, and $C_2$ have radii $r$, $r_1$, and $r_2$, respectively, then I think that $(x,y)$ is the intersection of the circle with radius $1-r$ and the hyperbola with focii at $(x_1, y_1)$ and $(x_2, y_2)$ and difference in distances $|r_1-r_2|$, but that doesn't help too much for determining the coordinates $(x, y)$.

Is there a better way of doing this?

Taha Akbari
  • 3,770
  • Do $C_1$ and $C_2$ intersect? If they do, it is useful to consider a circular inversion having centre in a point of intersection of $C_1$ and $C_2$. – Jack D'Aurizio Oct 11 '15 at 21:04
  • Sorry, I forgot to say that $C_1$ and $C_2$ should be tangent to each other. I'll edit the post to say that. –  Oct 11 '15 at 21:12
  • Oh, well, it works also in that case. Consider a circular inversion with respect to the tangency point of $C_1$ and $C_2$: the problem becomes to find a circle tangent to two lines and a circle. That can be solved by intersecting a parabola and a line. – Jack D'Aurizio Oct 11 '15 at 21:18
  • Have a look at http://www.mathpages.com/home/kmath113/kmath113.htm , in any case. – Jack D'Aurizio Oct 11 '15 at 21:19
  • 1
    This is the problem of Apollonius. – Lucian Oct 12 '15 at 02:15
  • @Lucian You're right, but its really a very special case of the problem of Apollonius: all three circles are tangent, and one of them is externally tangent. I can find the coordinates of the third circle if none are externally tangent, so I was hoping to get a way of doing it in this case as well. –  Oct 12 '15 at 20:38

1 Answers1

1

If we have circles with centers at $(0,0)$, $(x_1,y_1)$, and $(x_2,y_2)$, with radii $1$, $r_1$, and $r_2$ where $$ |(x_1,y_1)|=1-r_1\quad\text{tangent to unit circle} $$ $$ |(x_2,y_2)|=1-r_2\quad\text{tangent to unit circle} $$ $$ |(x_1,y_1)-(x_2,y_2)|=r_1+r_2\quad\text{tangent to each other} $$ Descartes' Theorem says that $$ \left(\frac1{r_3}+\frac1{r_2}+\frac1{r_1}-1\right)^2=2\left(\frac1{r_3^2}+\frac1{r_2^2}+\frac1{r_1^2}+1\right)\tag1 $$ Equation $(1)$ allows us to compute two values for $r_3$.

Using the Corollary to the Soddy-Gosset Theorem proven in this answer, we have $$ \frac{\frac{(x_3,y_3)}{r_3^2}+\frac{(x_2,y_2)}{r_2^2}+\frac{(x_1,y_1)}{r_1^2}}{\frac1{r_3^2}+\frac1{r_2^2}+\frac1{r_1^2}+1} =\frac{\frac{(x_3,y_3)}{r_3}+\frac{(x_2,y_2)}{r_2}+\frac{(x_1,y_1)}{r_1}}{\frac1{r_3}+\frac1{r_2}+\frac1{r_1}-1}\tag2 $$ Equation $(2)$ allows us to compute one value of $(x_3,y_3)$ for each value of $r_3$ computed in $(1)$.

Example

enter image description here

The two solutions to $(1)$: $$ \left(2+3+\color{#C00}{6}-1\right)^2=100=2\left(2^2+3^2+\color{#C00}{6}^2+1^2\right) $$ and $$ \left(2+3+\color{#C00}{2}-1\right)^2=36=2\left(2^2+3^2+\color{#C00}{2}^2+1^2\right) $$ That is, the radii are $\frac16$ and $\frac12$.

Then, the centers can be computed $$ \begin{align} &\frac{-1(0,0)+2\left(\frac12,0\right)+3\left(0,-\frac23\right)+\color{#C00}{6\left(\frac12,-\frac23\right)}}{-1+2+3+\color{#C00}{6}}\\ &=\left(\frac25,-\frac35\right)\\ &=\frac{1^2(0,0)+2^2\left(\frac12,0\right)+3^2\left(0,-\frac23\right)+\color{#C00}{6^2\!\left(\frac12,-\frac23\right)}}{1^2+2^2+3^2+\color{#C00}{6^2}} \end{align} $$ and $$ \begin{align} &\frac{-1(0,0)+2\left(\frac12,0\right)+3\left(0,-\frac23\right)+\color{#C00}{2\left(-\frac12,0\right)}}{-1+2+3+\color{#C00}{2}}\\ &=\left(0,-\frac13\right)\\ &=\frac{1^2(0,0)+2^2\left(\frac12,0\right)+3^2\left(0,-\frac23\right)+\color{#C00}{2^2\!\left(-\frac12,0\right)}}{1^2+2^2+3^2+\color{#C00}{2^2}} \end{align} $$ That is, the center for the circle with radius $\frac16$ is $\left(\frac12,-\frac23\right)$ and the center for the circle with radius $\frac12$ is $\left(-\frac12,0\right)$.

robjohn
  • 353,833