3

I'm not sure how to solve this inequality. Can someone please explain step-by-step? Thanks!

$ |x| + |x - 2| \gt 5 $

关一骏
  • 485
  • Do I subtract the $5$ from both sides? I don't even know how to start. – 关一骏 Oct 10 '15 at 02:11
  • You need to identify all cases where the signs change in the terms: e.g., $x<0,x<2$ so you have 3 scenarios to think about (including $x>2$). –  Oct 10 '15 at 02:13
  • 1
    We can use algebra. Or else draw a number line with fat dots at $0$ and $2$. When we say $|x|+|x-2|\gt 5$, we are saying the sum of the distances of $x$ from $0$ and from $2$ is $\gt 5$. That will happen if we are more than $1.5$ units to the right of $2$, or more than $1.5$ units to the left of $0$. – André Nicolas Oct 10 '15 at 02:25
  • You can find some similar posts if you browse other questions tagged inequality+absolute-value. They might be useful for you, if you are working on this type of problems. – Martin Sleziak Oct 10 '15 at 12:14

3 Answers3

3

If $x \geq 2$, then $|x| + |x-2| = 2x-2$, which is $ > 5$ iff $x > \frac{7}{2}$. If $0 \leq x < 2$, then $|x| + |x-2| = x+2-x = 2 < 5$. If $x < 0$, then $|x| + |x-2| = -x+2-x = 2-2x$, which is $> 5$ iff $x < \frac{-3}{2}$.

Do you then know how to conclude?

Yes
  • 20,910
2

When in doubt it's always best to draw a sketch.

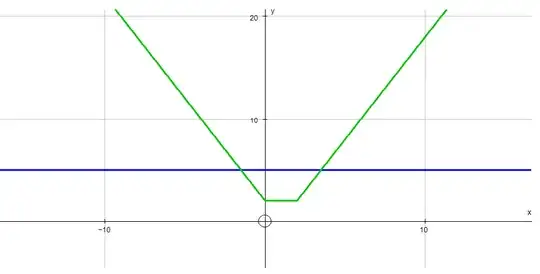
The Blue line is $y=5$.

The Green line is $y=|x|+|x−2|$

I know this is not a rigorous answer for you, but I just thought it may help to show you the graph of your function.

You can see from the two intersecting points that $|x|+|x−2| \gt 5$ above those two points. enter image description here

BLAZE
  • 1
-2

Since $\mid x\mid$ and $\mid{x-2}\mid$ will always be positive, you can change the equation to $x+x-2 \gt 5$. This gives you $2x-2\gt 5$ then $2x \gt 7$ and the final answer is $x \gt \frac72$ Also since x can be negative you must set another equation as $|x|+|x-2| \lt -5$ and solve this as $x+x-2 \lt -5$ and get $2x-2 \lt -5$ then $2x \lt -3$ then $x \lt -\frac{3}{2}$ so $x \gt \frac72$ or $x \lt -\frac{3}{2}$

BLAZE
  • 1
Spartan 117
  • 21
  • 2
    That's funny, because $x=-10$ works too. Just a random example. – Integral Oct 10 '15 at 02:31
  • Sure $|x|$ is always non negative, but it's only equal to $x$ when $x$ itself is non negative (otherwise it's equal to $-x$). The same goes for $|x-2|$. So $|x|+|x-2|$ could possibly be equal to any $4$ possible combination of signs $\pm x + \pm (x-2)$, and you have to look at those other cases. – Joel Cohen Oct 10 '15 at 02:38
  • In interval notation, your x can either be (7/2,inf) or (-inf,-3/2) that is if you set another |x|+|x-2| <-5 to account for the fact that x can be negative. – Spartan 117 Oct 10 '15 at 02:40
  • 1
    @Joel Do me a favour and learn how to format your working please, that's twice I've edited it now, here is the best place to learn – BLAZE Oct 10 '15 at 02:51