1

A cycloid is a flat curve that is traced by point of the rim of a circle while the circle rolls without slippage on the line. Show that if the line is the axis $x$ and the circle has radius $a>0$, then the cycloid can be parametrized by $$\gamma (t)=a(t-\sin t, 1-\cos t)$$ Could you give me some hints how we could show that? I don't really have an idea what I could do...

J. M. ain't a mathematician
  • 76,540
Mary Star
  • 14,186
  • 15
  • 91
  • 205
  • 1
    possible duplicate: http://math.stackexchange.com/questions/133604/how-to-find-the-parametric-equation-of-a-cycloid – Emilio Novati Sep 29 '15 at 20:28
  • 1
    @Mary Star Certainly a duplicate. I looked at it and instantly gave my vote because of that lovely animation! Check it out, Mary – imranfat Sep 29 '15 at 20:35

1 Answers1

1

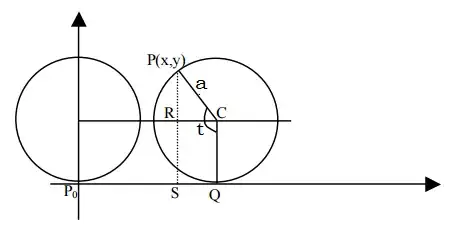
I give you here (with weak English) an explanation of the parametric you ask. In the figure below, your point $P(x,y)$ has started from the position $P_0$ at the coordinate origin.

By definition of cycloid the arc $\widehat{PQ}$ subtended by the angle $t$ (which is choose as parameter!) and the segment $\overline{P_0Q}$ have the same length equal to $at$. Now all is easy: $$x=\overline {P_0Q}-\overline{SQ}=at-a\space cos(t-\frac{\pi}{2})=a(t-sin\space t)$$ $$y=\overline{SP}=\overline{SR}+\overline{RP}=a+a\space sin(t-\frac{\pi}{2})=a(1-cos\space t)$$

enter image description here

Ataulfo
  • 32,657
  • 1
    It is not strictly necessary but it's better, for understanding, if you let see first that the function is clearly periodic with period 2 $\ pi$ with which you work in the interval [0,2$\pi$] – Ataulfo Sep 30 '15 at 00:10
  • Why does it stand that the length of the segment $\overline{P_0Q}$ is equal to $at$ ? – Mary Star Oct 02 '15 at 13:50
  • 1
    This is simply the formule for the arc of a circunference, it is known equal to $r\alpha$ where $r$ is the radius and $\alpha$ is the angle which subtends the arc. – Ataulfo Oct 02 '15 at 16:53
  • Why is this segment equal to the arc of a circumference? – Mary Star Oct 02 '15 at 17:11
  • 1
    By the very definition of cycloide. When the point $P(x,y)$ touch again the X-axis the circumference has crossed exactly a lenght equal to its lenght $2a \pi$. It is maybe clearer if you make back the point till the origin (it seems to me more "intuitive" because of the condition "without slippage"). – Ataulfo Oct 02 '15 at 19:39
  • Ok... Thank you very much!! :-) – Mary Star Oct 05 '15 at 21:32