I was trying to understand the proof (the introduction to the proof actually) made in Bredon's book when I encountered a problem in this passage (Page 349)
Suppose that $(K,L)\subset(U,V)$ as above (i.e. $K$ compact closed subset of a fixed orientable $n$-manifold $M$, $L \subset K$ closed $V\subset U$ opens.) Then there is a cap product $$ \Delta^p(U,V;G)\otimes \left[ \frac{\Delta_n(V)+\Delta_n(U\setminus L)}{\Delta_n(U\setminus K)} \right] \xrightarrow{\cap} \Delta_{n-p}(U\setminus L,U\setminus K;G)$$ given by $f\cap(b+c)=f\cap b+ f\cap c = f\cap c$. Note that in homology $$H_{n-p}(U\setminus L, U \setminus K) \cong H_{n-p}(M\setminus L,M\setminus K)$$. Also $$H_*\left( \frac{\Delta_*(V)+\Delta_*(U\setminus L)}{\Delta_*(U\setminus K)}\right)\cong H_*(U,U\setminus K) \cong H_*(M,M\setminus K)$$ by excision and since $\{V,U\setminus L\}$ is an open cover of $U$. Thus in (co)homology we get a cap product $$H^p(U,V;G)\otimes H_n(M,M\setminus K) \to H_{n-p}(M\setminus L,M\setminus K;G)$$ Also, this is natural in $(K,L)$ (fulfilling the restrictions it must). In particular one can cap with a class in $H_n(M,M\setminus A)$ for some very large compact set $A$
First Question:I don't understand what does the author mean with natural in $(K,L)$ where in this cap product the only place where $K$ (resp. $L$) appear is $M\setminus K$ (resp. $M\setminus L$). I don't fully understand the sentence in brackets, which I think, is meant to explain naturality. I tried to apply the "naturality" of the cap product: so I considered the map $$restr\colon (M,M\setminus K) \to (M,M\setminus A)$$ and obtained such commutative diagram:
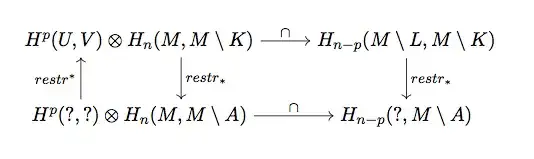
where the question marks, stress the fact that I don't know how rest, behave on the opens $U$ and $V$ and $M\setminus L$.
Second Question: why we need this naturality to affirm: "In particular one can cap with a class in $H_n(M,M\setminus A)$ for some very large compact set $A$"?
What I did From what I understand, being natural in $(K,L)$ means that, given a map $\varphi \colon (K,L) \to (K',L')$ then the the obvious diagram (upper row with $K,L$, lower row with $K',L'$) commute, but here firstly I have to assume that $\varphi$ extends to a map $\bar{\varphi} \colon M \to M$ otherwise I don't know how to get a map from $M\setminus K \to M\setminus K'$ (and I fear my hypothesis are not strong enough to ensure existence of such restriction).