This is a question related to the last one I asked yesterday: Ratio of Areas of Quadrilateral
Again I tried to make use of the same theorem (*) but have failed. I believe this time the question is not problamatic, thanks for help.
I think this fact play a key role: If the line $AB$ and $PQ$ intersect at $M$, then $[ABP]/[ABQ]=PM/QM$.
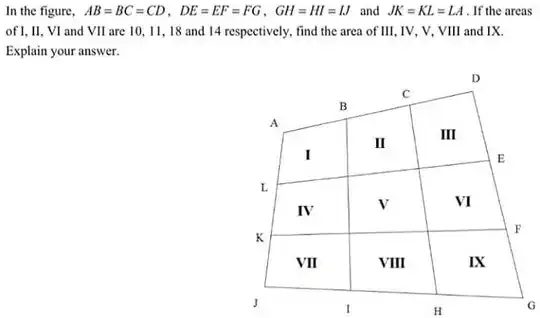
Let's take point $J$ as the origin of a coordinate system, and point $I$ on the $x$-axis. The coordinates of all points can be expressed in terms of five parameters: $I_x$, $K_x$, $K_y$, $D_x$, $D_y$. The same goes for the areas of all the nine quadrilaterals. So we are given four equations (as four areas are given by the text) to find five parameters: I've just tried to solve this system with the help of Mathematica but no solutions can be found. So the problem is impossible.
One wonders then what kind of solution were the authors expecting. I think they expected us to use the theorem given on page 6 here: if two opposite sides of a quadrilateral are trisected and corresponding points joined, then three new quadrilaterals are formed, and the area of the central one is the average of the areas of the other two.
Applying that to our problem without thinking too much would immediately lead to a supposed solution, with areas 10, 11, 12; 12, 15, 18; 14, 19, 24. But this is of course a fake solution, because the inner lines are NOT trisected.
