Algebraic Topology Question Regarding a Space

Question

I recently encountered the following:

Let $X_i$ for $i = 1,2$ be $S^1$ x $D^2$, where $S^1$ is the circle and $D^2$ is the disk. Let f be the homeomorphism from the boundary of $X_1$ to the boundary of $X_2$. f: $S^1$ x $∂D^2 \cong ∂D^2$ x $S^1$ (i.e. f just interchanges the factors of the product). Let Z be the disjoint union of $X_1$ and $X_2$ over f. Compute $π_1(Z)$, and describe the universal cover of Z. Note $π_1(Z)$ represents the fundamental group of Z.

I do not understand what the disjoint union of $X_1$ and $X_2$ over f represents. Could someone help me out? I believe it is $S^1$ x $D^2$ x $S^1$.

Answer 1

Note that a thickened neighborhood of each $X_i$ for $i = 1,2$ open covers $X_1 \cup_f X_2$. Let the open cover we constructed be $\{U, V\}$. $U$ and $V$ deformation retracts to $X_1$ and $X_2$ respectively. Note that $U \cap V$ is the boundary torus of $X_i$, hence $i_U : \pi_1(U \cap V) \to \pi_1(U)$ takes the meridian to $0$ and longitude to $1$ and $i_V : \pi_1(U \cap V) \to \pi_1(V)$ takes the meridian to $1$ and longitude to $0$.

Hence, the relators make the generators vanish. Thus, by Siefert-van Kampen theorem, we conclude $\pi_1(X_1 \cup_f X_2) \cong 0$.

A straight-forward "cheat" to do these problems is to determine the homotopy type of the adjunction space. In this case, $X_1 \cup_f X_2$ is actually homeomorphic to $S^3$. To see this, consider a solid torus in $\Bbb R^3$. Take the complement. This also looks somewhat like a genus $1$ thing. Indeed, compactifying precisely gives you a torus. Thus, $S^3$ can be decomposed into two tori glued precisely by the homeomorphism you mention (you should be able to see this with some practice).

Here's a sketch to help you see this (from this answer) :

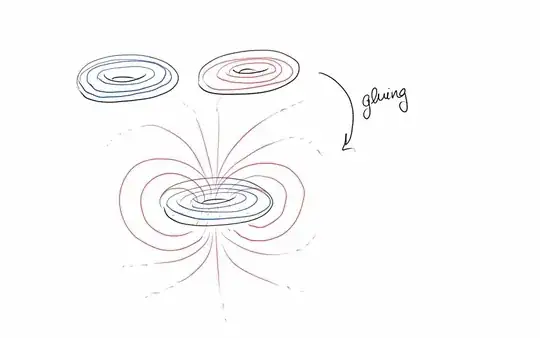
Thus, $\pi_1(X_1 \cup_f X_2) \cong \pi_1(S^3) \cong 0$.

As a side-note, decomposing $3$-manifolds into solid genus $g$ surfaces (usually called handlebodies) is called Heegaard decompositon for the $3$-manifold. It is known that every $3$-manifold admits a Heegaard decomposition. Thus, the problem of computing $\pi_1$ of $3$-manifolds in general becomes a problem of determining the homeomorphism by which the handlebodies are glued along.

Answer 2

To complement the last answer. let $S^3$ be represented by points $(x_1,\ldots,x_4) \in \mathbb R^4 $ such that $x_1^2 +\cdots +x_4^2=1$. Then the subspace $A$ of $S^3$ of points such that $x_1^2 + x_2^2\leqslant 1/2 $ is homeomorphic to $D^2 \times S^1$, and the subspace $B$ of points such that $x_1^2 + x_2^2\geqslant 1/2 $ is homeomorphic to $S^1 \times D^2$, while the subspace $A \cap B$ is homeomorphic to $S^1 \times S^1$.