3

I am trying to solve the following problem and have looked at similar problems with different initial conditions but I am still having trouble piecing everything together. Here is the question:

Consider the initial value problem

$u_t + uu_x=0, \quad x \in \mathbb{R},\quad t>0$

$u(x,0)=\begin{cases} 1-x^2 & |x|\leq1 \\ 0 & |x|>1 \end{cases}$

Sketch the characteristic diagram. At what time $t_b$ does the wave break? Find a formula for the solution.

This is what I have so far:

$\frac{dx}{dt} = u(x,t) = \phi(\xi) \quad$ where $\quad \phi(x)=u(x,0)$ and $\xi \in \mathbb{R}$.

Hence, for $|\xi| \leq 1 \quad \frac{dx}{dt} = 1-\xi^2 \implies x = t-t\xi^2 = t(1-\xi^2)$

and for $|\xi| > 1 \quad \frac{dx}{dt} = 0 \implies x = \xi$

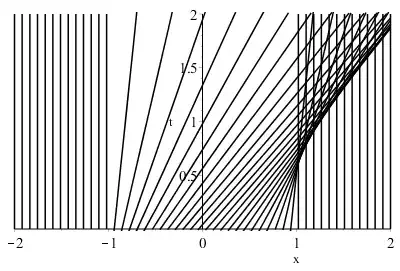
Therefore I think I can draw the following (rough) characteristic curves. 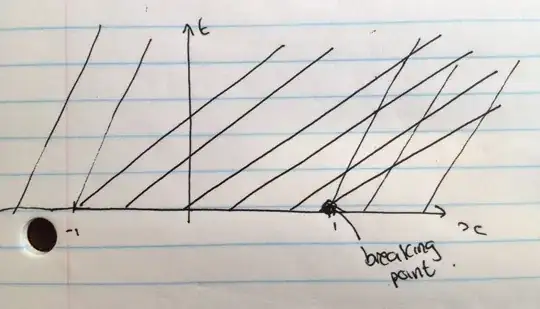enter image description here I'm not sure if this is correct though so please let me know if this is wrong.

Also I tried to find the solution, that is:

Knowing that $x = t-t\xi^2$ in the $|\xi|\leq1$ case, we can show that $\xi = \sqrt{\frac{t-x}{t}}$ and hence $u(x,t)=\phi(\xi)=1-\left( \sqrt{\frac{t-x}{t}}\right)^2=\frac{x}{t}$.

And similarly, in the $|\xi|>1$ case, $u(x,t)=0$

So $u(x,t)=\begin{cases} \frac{x}{t} & |x|\leq1 \\ 0 & |x|>1 \end{cases}$

I then need to work out the breaking time which I have tried to do but don't have an answer.

If you can help I'd be very appreciative.

EditPiAf
  • 21,328
Daniel Ward
  • 377

1 Answers1

4

Here is a sketch of the characteristic curves $x = \phi(x_0)t + x_0$, where $\phi(x) = u(x,0)$:

characteristics

As specified in this post, the breaking time is $t_b = {-1}/{\inf \phi'} = {1}/{2}$, which corresponds to the time where characteristics intersect in the figure. For times $t< 1/2$, the solution is given by the method of characteristics, i.e. $u = \phi(x-ut)$: $$ u(x,t) = \left\lbrace \begin{aligned} &\frac{2 t x - 1 + \sqrt{4 t^2 - 4 t x + 1}}{2 t^2} &&\text{if}\; |x| \leq 1 \\ &0 && \text{otherwise} \end{aligned}\right. $$ For larger times, this solution is no longer valid. The shock trajectory $x_s(t)$ satisfies the Rankine-Hugoniot condition $$ \dot x_s = \frac{1}{2}\left(\frac{2 t x_s - 1 + \sqrt{4 t^2 - 4 t x_s + 1}}{2 t^2} + 0\right) ,\qquad x_s(1/2) = 1 . $$ Even if I don't know any exact analytical solution to this differential equation, the solution for $t\geq 1/2$ reads $$ u(x,t) = \left\lbrace \begin{aligned} &\frac{2 t x - 1 + \sqrt{4 t^2 - 4 t x + 1}}{2 t^2} &&\text{if}\; {-1}\leq x < x_s(t) \\ &0 && \text{otherwise} \end{aligned}\right. $$

EditPiAf
  • 21,328