2

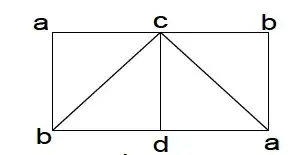
enter image description here

On the surface, it looks like it would be a Mobius Strip due to the "twist".

However, there are some inconsistencies like b is adjacent to d on the left, but not on the right of the figure.

Hence, is this a valid triangulation of a space by a labeled complex?

Thanks a lot!

yoyostein
  • 20,428

1 Answers1

3

Your diagram is a good CW complex (whose underlying space is indeed the Moebius strip) but it is not a good simplicial complex: in a simplical complex the intersection of any two simplices is required to be a simplex. You have two triangles labelled $abc$ whose intersection is the edge $ab$ and the vertex $c$. It is standard to require a triangulation to give a simplicial complex, e.g., see https://en.wikipedia.org/wiki/Triangulation_(topology).

The term "pseudo-triangulation" was used in this discussion Triangulation of Torus. The proposed triangulation in that discussion identifies vertices of some triangles, so it's more obviously not a simplicial complex than your example.

Community
  • 1
Rob Arthan
  • 51,538
  • 4
  • 53
  • 105
  • If we identify points b with b, wouldn't bc be a common intersection as well? – yoyostein Aug 30 '15 at 15:43
  • I was assuming you were just identifying $ab$ with $ba$ like you would if you were making a Moebius strip out of paper (and so that the result if a surface - i.e., a $2$-manifold). If you do those extra identifications, you get something that is not topologically equivalent to a Moebius strip. – Rob Arthan Aug 30 '15 at 15:50