8

Background

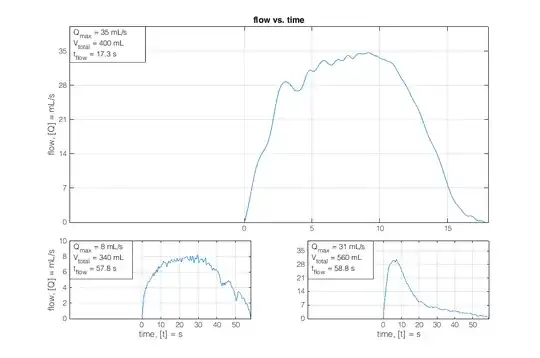
I'm analysing a data set of $M$ flow measurements (volume per time). The flows go from zero mL/s gradually to higher values and back to zero again, thus: their shapes ideally look like a Gaussian (or bell-shaped) curve. However, their shapes vary: they can go up and down (a little or a lot) over time. See the figure below for three examples.

three demo flows

The variations in the shapes are what I'm interested in. I'm using principal component analysis (PCA) in MATLAB for this purpose, with which I hope to find a (small) number of basic patterns that explain these variations in the flow curve shapes.

Note the following important steps I take: I interpolate the time axis, so all flows have an equal number of samples and all flows begin on $n=1,\,n\in N$ and end on $n=N$. I do this because I care only about shape, without time being of influence.

The data matrix $A$ I analyse with PCA has $M$ rows (observations) and $N$ columns (samples).

PCA

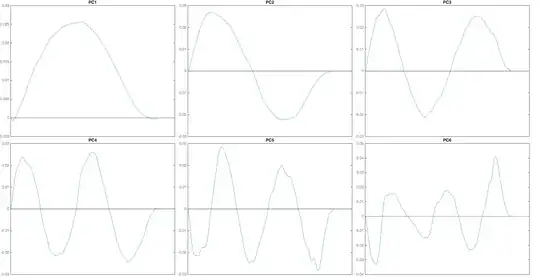
When I perform PCA on the aforementioned data, I get a quite peculiar result. I doubt it is by chance. The principal components (PCs) appear to be sinusoids, more or less. The first PC is a half period (positive) of a sinus, resembling the basic shape I describe in the first paragraph of this question. It is not a perfect sine, as it contains some variation. The second component is a full period of a sine: it goes up from zero, back to and through zero and becomes negative to then go back up to zero again. The third PC is one-and-a-half period, etc. See the figure below for the first 6 PCs (of $M=657$ flows).

first 6 PCs

I feel this has a connection with the Fourier series, because my principal components basically appear to be the frequency components of my original data, or are related to them. Is there an intuitive way (and a mathematical way, of course), to understand why I get this particular result? I guess the sinusoids are in fact the result of the relation between PCA and the Fourier series and the variation in the sinusoids is caused by the variations/noise in my data.

Rodrigo de Azevedo
  • 23,223
Erik
  • 605
  • Maybe you could illustrate what you're observing with some pictures? I sampled a gaussian with randomly selected deviation in $[0.5, 1]$ over the interval $[-3,3]$ using $N=128$ uniformly spaced points. I did this 512 times each with different randomly selected deviation. The resulting principle components did not look like sinusoids, but rather even derivatives of gaussians... – Chester Aug 10 '15 at 12:26
  • @Chester - I've added some images. Thanks for trying to reproduce my results without any example. Your Gaussians aren't working, because they don't start to rise significantly after the first sample. I guess my description of the shape with the word Gaussian wasn't perfect, but the fact remains that many curves do resemble a Gaussian curve, albeit they start and end with zero mL/s (which a Gaussian never reaches). – Erik Aug 10 '15 at 18:55
  • 1
    Interesting! Well, I won't pretend to understand this. Although, you may want to add the "stochastic-processes" tag to your post. In fact, there is a functional PCA which deals in stochastic processes that may be worth looking into... In any case, it seems like there is some cool stochastic process and/or functional analysis going on underneath here. Hopefully someone else can provide some insight :) – Chester Aug 10 '15 at 19:43

1 Answers1

10

This is a typical result if you have data that are characterized by a localized and approximately stationary autocorrelation. Here's a simple demonstration in Matlab.

Generate mutually uncorrelated time series of white noise:

M = 100;          % number of variables
N = 1000000;      % number of samples (time points)
x = randn(N, M);

Induce autocorrelation across variables ("flows") by computing a moving average (implemented here using a Toeplitz matrix):

ma = toeplitz([ones(1, 5) zeros(1, M - 5)]);
x = x * ma;

Compute the PCA and plot the first principal modes:

[v, e] = eig(cov(x));
[e, ind] = sort(diag(e), 'descend');
v = v(:, ind);
plot(v(:, 1 : 3), '.-')
xlabel('variables')
legend({'PM1', 'PM2', 'PM3'})

The result looks like this:

The reason is that data with stationary autocorrelation can be seen as being generated by a linear translation-invariant operator (often "time-invariant", but here the relevant dimension is "variable", not "time"), i.e. by a convolution process, and the eigenvectors of such an operator are the harmonic functions. The eigenvectors of the covariance matrix (the principal modes) are estimates of the eigenvectors of the operator because the true covariance is identical to the product of the operator matrix with itself. — Here the actual operator is given by the Toeplitz matrix, which is only almost translation-invariant (because of the boundaries), so we get almost-harmonic functions.

Btw., I used the term "principal modes" above because the term "principal components" usually refers to that aspect of PCA which is a function of the dimension across which the covariance matrix has been computed; here, time. The principal components are obtained by transforming the data into the base spanned by the principal modes.

A. Donda
  • 1,466
  • What do you mean by ‘the eigenvectors of such an operator’ (a convolution process). In your example, do you mean the eigenvectors of your Toeplitz matrix ma, because the ones(1,5) is a moving average of five samples (the LTI operation)? I'll try to plot the eigenvectors of ma to see what they look like. – Erik Aug 10 '15 at 20:07
  • 1
    Yes, in my example the relevant operator is the Toeplitz matrix ma. And yes, the moving average is the LTI operation. The eigenvectors of ma should look like those of the covariance matrix, only slightly nicer because ma is not just an estimate. I used a large value of N to get a good covariance estimate. – A. Donda Aug 10 '15 at 20:11
  • @Erik, a question: Have your M different "flows" been measured at something like adjacent positions? If yes, that would explain the localized, approximately stationary autocorrelation. – A. Donda Aug 10 '15 at 20:13
  • Actually, my PC ran out of memory with N=1000000, but removing a zero solved the problem. ;) – Erik Aug 10 '15 at 20:16
  • 1
    The flows are all from independent sources, but the sources apparently share some similar underlying behaviour, else I wouldn't get my somewhat sinusoidal results. I wonder how I can further find out what the underlying mechanics are. – Erik Aug 10 '15 at 20:18
  • @Erik, thanks for the accept. Regarding your comment, it is really hard to say anything more without knowing more about the experiment. There are plenty of possible mechanisms... – A. Donda Aug 11 '15 at 18:50