5

Along the lines of my lines of my previous question about irrational angles "$45^\circ$ Rubik's Cube: proving $\arccos ( \frac{\sqrt{2}}{2} - \frac{1}{4} )$ is an irrational angle?", I was working on a puzzle and I ran into an interesting question about an irrational angle.

Take a puzzle made out of a triangular bipyramid that turns on its vertices: constellation 6 puzzle

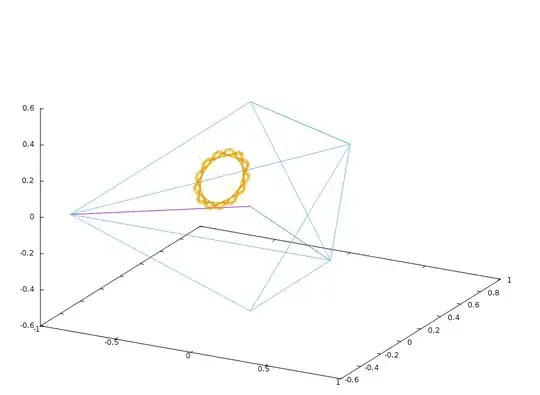
The piece in the center must be a circle because it gets rotated by an irrational amount after some combination of moves. Here is the path a point takes after repeatedly turning the purple axis followed by the green axis 90 degrees: point path after 90L 90R

The rotation matrix for this operation is $$\left( \begin{array}{ccc} \frac{1}{8} & \frac{3}{4} & \frac{3}{8}\sqrt{3} \\ \frac{-3}{4} & \frac{1}{2} & \frac{-1}{4}\sqrt{3} \\ \frac{-3}{8}\sqrt{3} & \frac{-1}{4}\sqrt{3} & \frac{5}{8} \end{array} \right)$$

From there you can find the axis that points are rotating around is $[0, \sqrt{3}/2, -1]$ And the angle $\theta$ they're rotating through is $\arccos{\frac{1}{8}}$.

$\arccos{\frac{1}{8}}$ is approximately $82.819244218541^{\circ}$ and it's an irrational angle because the only rational values that correspond to rational angles for $\cos{\theta}$ are $\{-1, \frac{-1}{2}, 0, \frac{1}{2}, 1\}$.

So what do we know about $\theta = \arccos{\frac{1}{8}}$? It's irrational angle but is it an algebraic angle? In general if $\cos \theta$ is rational does that tell us anything (beyond rationality) about $\theta$?

Community
  • 1
Brandon Enright
  • 483

1 Answers1

4

The Gelfond-Schneider theorem says if $a\notin \{0,1\}$ is algebraic and $b$ is algebraic and irrational, then $a^b$ is transcendental. Apply this to $a = e^{i\pi/180}$, and you find that if $b$ is an irrational algebraic, $\omega = \cos(b^\circ) + i \sin(b^\circ)$ is transcendental. Then $\cos(b^\circ) = (\omega + \omega^{-1})/2$ and $\sin(b^\circ) = (\omega - \omega^{-1})/(2i)$ are also transcendental.

Nicholas Pipitone
  • 1,202
Robert Israel
  • 470,583
  • Your answer is a bit over my head so I'm going to have to do more reading before I understand it. Thank you, it's going to take me a while to accept though :-) – Brandon Enright Aug 03 '15 at 03:38
  • Alright I think I follow the first part. You choose $a = e^{i \pi / 180}$ because it corresponds to $\cos({\frac{\pi}{180}}) + i\sin({\frac{\pi}{180}})$ and $\frac{\pi}{180}$ is a rational angle so $a$ would have to be algebraic. Then $a^b$ would be $e^{i\pi b / 180}$ which treats $b$ as irrational degrees and establishes the transcendence of $\cos(b^{\circ}) + i\sin(b^{\circ})$. I don't follow how you eliminated the $i\sin(b^{\circ})$ term though. How does raising $\omega$ to the $-1$ power do that? – Brandon Enright Aug 03 '15 at 03:57
  • @BrandonEnright: $(\cos(x) + i \sin(x))(\cos(x) - i \sin(x)) = \cos^2(x) + \sin^2(x) = 1$. – Robert Israel Aug 03 '15 at 04:35
  • Got it. You multiplied the numerator and denominator of $\omega^{-1}$ by $\cos(b^{\circ}) - i\sin(b^{\circ})$ which eliminates the denominator and leaves $\cos(b^{\circ}) - i\sin(b^{\circ})$ in the numerator and then the $i\sin(b^{\circ})$ terms cancel leaving $2\cos(b^{\circ})$ which you fix by dividing by 2. Whew I understand you answer now! – Brandon Enright Aug 03 '15 at 04:57