f∈c[a,b] (f is continuous in [a,b]), prove: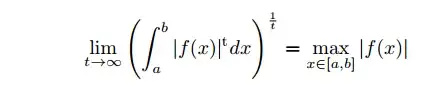
We tried to use the integral intermediate value theorem to try to prove it but we don't understand why the limit has to be the max and not any other value of f.
Thanks
f∈c[a,b] (f is continuous in [a,b]), prove: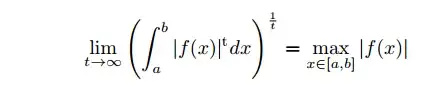
We tried to use the integral intermediate value theorem to try to prove it but we don't understand why the limit has to be the max and not any other value of f.
Thanks
Below follows an answer like the one here, but maybe with easier terminology. I will update if I find a simpler argument.
Let $M=\max_{x\in[a,b]}|f(x)|$ (which exist since $f$ is continuous and $[a,b]$ is compact).
To show $\leq$, note that, since $|f(x)|\leq M$ for all $x\in[a,b]$, $$ \Bigl(\int_a^b |f(x)|^t\,dx\Bigr)^{1/t}\leq \Bigl(\int_a^b M^t\,dx\Bigr)^{1/t}=M(b-a)^{1/t}. $$ In the limit $t\to+\infty$, we have $(b-a)^{1/t}\to 1$, and hence (one could do this more precise if needed) $$ \lim_{t\to+\infty}\Bigl(\int_a^b |f(x)|^t\,dx\Bigr)^{1/t}\leq M=\max_{x\in[a,b]}|f(x)|. $$
To show $\geq$, we let $0<\epsilon<M$ ($\epsilon$ arbitrary, but fixed below), and divide the interval into two disjoint parts, $$ I_1=\{x\in[a,b]~:~|f(x)|\geq M-\epsilon\} $$ and $$ I_2=[a,b]\setminus I_1=\{x\in[a,b]~:~|f(x)|<M-\epsilon\}. $$ Now, by throwing away the $I_2$ part, and using the fact that $|f(x)|\geq M-\epsilon$ when $x\in I_1$, $$ \Bigl(\int_a^b |f(x)|^t\,dx\Bigr)^{1/t} \geq \Bigl(\int_{x\in I_1}|f(x)|^t\,dx\Bigr)^{1/t} \geq \Bigl(\int_{x\in I_1}(M-\epsilon)^t\,dx\Bigr)^{1/t}. $$ The integrand in the right integral is constant, and thus can be calculated to be $$ (M-\epsilon)\mu(I_1)^{1/t}, $$ where $\mu(I_1)$ denotes the measure (think: total length, in the case you are not familiar with measure theory) of $I_1$. Since $\mu(I_1)>0$, taking the limit as $t\to+\infty$, $$ \lim_{t\to+\infty}\mu(I_1)^{1/t}=1, $$ and hence $$ \lim_{t\to+\infty}\Bigl(\int_a^b |f(x)|^t\,dx\Bigr)^{1/t}\geq M-\epsilon. $$ The wanted inequality follows by letting $\epsilon\to0^+$.