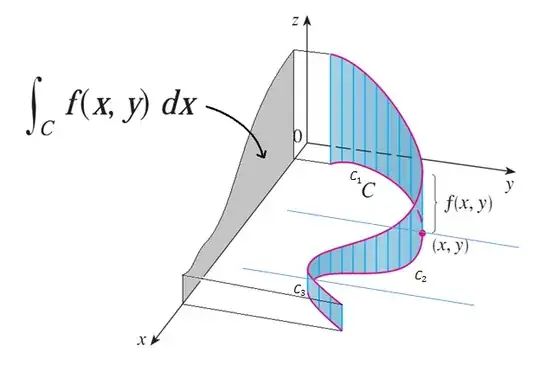
I'm studying the line integral of a function along a curve $C$ with respect to $x$. Is the assertion as the following figure indicated true or false?
I have read the questions Interpreting Line Integrals with Respect to $x$ or $y$ and Interpretation of a line integral with respect to x or y . But I am dissatisfied the answer.
And we can't give a geometrical interpretation of the line integral with respect to $y$ in this case because the direct of $y$ back and forth when $t$ increase.
As you said the curve back and forth in $y$ direction. Let's assume the curve $C$ does not have that little twist in $x$ direction at the beginning. This means the curve $C$ is a function of $x$.
Then the line integral with respect to $x$ would be $$\int_{x_1}^{x_2} f(x,y(x))\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx$$
where $\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx$ is the infinitesimal arc length of each subinterval. So it is exactly as in the picture.
Now for the $y$ direction, since $C$ is not really a function in this direction, we have to separate it into parts. In this case, we have three parts $C_1,C_2,C_3$, as shown below
On each subcurve, we can do the same thing as before:
$$\int_{y_1}^{y_2} f(x(y),y)\sqrt{1+\left(\frac{dx}{dy}\right)^2}\,dy$$
where $\sqrt{1+\left(\frac{dx}{dy}\right)^2}\,dy$ is the arc length of an subinterval.
