If $C$ is midpoint-convex and closed then it is a convex set

Question

Midpoint convexity. A set $C$ is midpoint convex if whenever two points $a, b$ are in $C$, the average or midpoint $(a + b)/2$ is in $C$. Prove that if $C$ is closed and midpoint convex, then $C$ is convex.

---

Convex set means that $\forall x_1, x_2 \in C, \theta x_1+(1-\theta)x_2 \in C \forall \theta \in[0,1]$

I know $$ \left(x_1+x_2\right)/2 \in C \implies \dfrac{x_1+\dfrac{x_1+x_2}{2}}{2}= \dfrac{x_1}{2}+\dfrac{x_1}{4}+\dfrac{x_2}{4} = \dfrac{3}{4}{x_1} + \dfrac{1}{4}{x_2} \in C $$ Applying this k times I get the following: $$ (1-2^{-k})x_1+2^{-k}x_2=(1-\theta_k)x_1+\theta_k x_2 \in C $$

but I have showed it only for $\theta$ values that takes the form of $2^{-k}$ where $k \in N$

What should I do next?

Answer 1

Let $t \in [0, 1]$.

We can construct a sequence of intervals such that $t$ is the only point in their intersection.

• $C_0 = [0, 1]$, $t \in X_0$
• Let $X_{i} = [a, b]$.
  • If $t \in [a, \frac{a+b}{2}]$, then $X_{i+1} = [a, \frac{a+b}{2}]$
  • If $t \in (\frac{a+b}{2}, b]$, then $X_{i+1} = [\frac{a+b}{2}, b]$

Obviously, it is a sequence of nested intervals, with $t$ being the only point in their intersection. Also, the bounds of the limits are constructed only taking midpoints of already constructed points. Taking only upper bound of this intervals, we get a sequence ${x_i}$ converging to $t$, and every element of the sequence is either $1$ or midpoint of some previous element of the sequence (and, probably, $0$).

Now, let $C$ be a closed and midpoint-convex set. Take any $a, b \in C$, $t \in [0,1]$. Our goal is to prove that $a (1 - t) + b t \in C$. Construct the discussed sequence $\{x_i\}$. Since $\{x_i\}$ is constructed taking midpoints, $\forall i \quad a (1 - x_i) + b x_i \in C$. Since $x_i \to t$, $a (1 - x_i) + b x_i \to a (1-t) + b t$. Since $C$ is closed, it contains limits of sequences of its elements. This proves that $a(1-t)+bt \in C$.

Answer 2

I propose here an intuitive argument that may be didactic for beginners.

Let $C$ be midpoint convex and closed, and consider any two points $x,y\in C$.

The intuition

To prove convexity, we need to prove that any $z=\lambda x + (1-\lambda)y$ with $\lambda \in [0,1]$ is in $C$.

Look at the image below. We are going to prove that it exist a sequence of midpoints $z_1, z_2,\ldots, z_k$ that converges to such point $z$. This sequence is built by computing, recurrently, the midpoint. On each iteration, we need to choose the closest midpoint to $z$, thus, sometimes we will take the left part of the segment $X_{l}^{k}$ and other times the right part $X_{r}^{k}$, just to ensure we approach $z$.

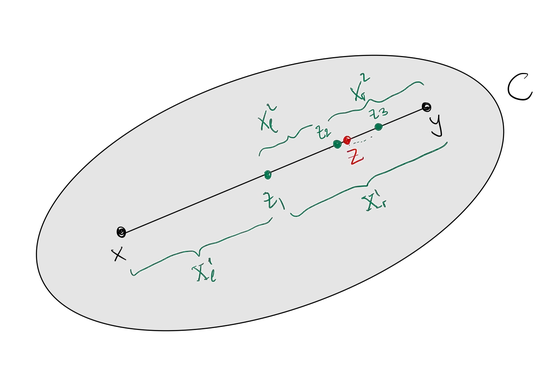
Following the intuition from the image, we build the first midpoint as:

$z_1 = (x+y)\frac{1}{2}=\frac{1}{2}x+\frac{1}{2}y$

Now, as $z \in X_{r}^{1}$, we choose the right part of the segment to continue the iteration:

$z_2=(z_1+y)\frac{1}{2}=(\frac{1}{2}x+\frac{1}{2}y + y)\frac{1}{2}=\frac{3}{4}x+\frac{1}{4}y$

Lets stop here. Here we figure out that the sequence of midpoints takes the form:

$z_k = \lambda_k x + (1-\lambda_k)y$

From the above example: $\lambda_1=\frac{1}{2}$, $\lambda_2 = \frac{3}{4}$...

Given that intuition, the coefficients take the following form:

$$\lambda_k = c_12^{-1}+c_22^{-2}+\ldots+c_k2^{-k}$$

where $c_i={0,1}$ is a bool number that means right (1) or left (0) choices to approach $z$.

In our example, we choose right on the first step:

$\lambda_1=1\cdot2^{-1}$

And right in the second, so:

$\lambda_2=1\cdot2^{-1}+1\cdot2^{-2}=\frac{3}{4}$

The proof

Now that we have the intuition lets do the formal math. We need to prove 1) that such $\lambda_k$ is convergent to a number lower or equal to 1 and 2) that the generated point is in $C$.

1.)Convergence

The sequence $z_k = x\lambda_k + y(1-\lambda_k)$ is convergent to a point $z=\lambda x + (1-\lambda)y \in C$.

As $c_k={0,1}$, we have that: $$0\le\lambda_k =\sum_{i=1}^{k}{c_i2^{-i}} \le \sum_{i=1}^{k}{2^{-i}} = \frac{1-\left(\frac{1}{2}\right)^k}{1-\frac{1}{2}}-1=2(1-2^{-k})-1 \le 1$$ Thus, the serie is majored by a convergent serie bounded to 1. Notice that $k=0$ corresponds to the trivial case where $z=x$ or $z=y$.

Lets say that $\lambda_k \rightarrow \lambda$ so that $z_k = \lambda_k x + (1-\lambda_k)y \rightarrow z = \lambda x + (1-\lambda)y$.

2.)Included

$C$ is a closed set, so it contains the limit of any sequence with elements in $C$. It ensures that the the point $z_k \rightarrow z \in C$.

QED :)

Extra Ball

We could interpret $\lambda_k=c_12^{-1}+c_22^{-2}+\ldots+c_k2^{-k}$ as the representation in base two (binary) of the decimal part of the real number $\lambda\in[0,1]$ as much exact as we want to, just by adding terms to the sum.