2

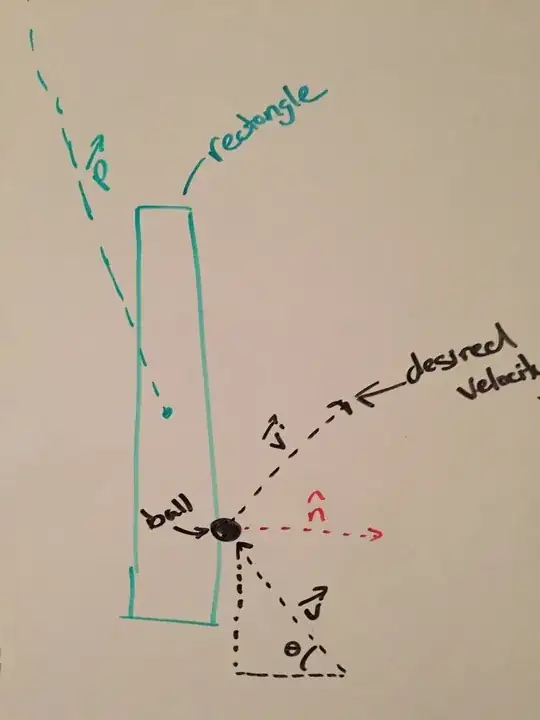
I hope this is not a stupid question. I am having a hard time finding a normal in $2D$. I am working on a game project and I am trying to perform vector reflection during collision. I know the rest of the math, but I am having a hard time creating the normal vector that is required.

Is there a way to build a normal vector from the point of collision? What do I need to create the normal vector?

My position vector does not necessarily point in the direction of the object. My position can be $(100, 200)$ but the object is a vertical object for example. What else can I do for this?

enter image description here

TShiong
  • 1,270
Ethosik
  • 121
  • 1
    I think you can upload your picture somewhere else and post a link – coldnumber Jul 19 '15 at 02:20
  • 1
    In two dimensions, a vector normal to the vector $(a,b)$ is $(-b,a)$ (or any multiple thereof). – Greg Martin Jul 19 '15 at 02:52
  • I added an image – Ethosik Jul 19 '15 at 16:47
  • How are you defining the collision surfaces? – K. Rmth Jul 19 '15 at 17:14
  • @K.Rmth Are you referring to the rectangle? That is built in to the game. It is the bounding rectangle of the image, so I am doing rectangular collision detection. I need a vector to get a normal right? I guess I can get a vector from the top right to the bottom right and get the normal from that. Is that the best option? – Ethosik Jul 19 '15 at 17:46
  • @Ethosik I wouldn't say it would be the best option, but it could work though. Try it out. – K. Rmth Jul 19 '15 at 17:49
  • @K.Rmth What would be the best option? Actually, the normal vectors will be the same always, so I just need to know what side the collision hit. If it is on the right side, the normal will be a vector pointing to the right always. I wouldn't need to constantly keep creating a vector in that case. Do you have another idea? As you can see, I cannot use the position vector since it comes from the top left. – Ethosik Jul 19 '15 at 18:00
  • You could use the position vector of both the rectangle and the object to determine which side of the rectangle is being hit. The normal is easily obtained as is the reflection vector. (see here) – K. Rmth Jul 19 '15 at 18:11
  • @K.Rmth The position vector for the rectangle and the object are the same. How would I adapt this for a rectangle instead of a circle? And is it an issue if the position of the object and rectangle are the same? Or are you referring to the position of the "ball" object? – Ethosik Jul 19 '15 at 18:16
  • Let us continue this discussion in chat. – K. Rmth Jul 19 '15 at 18:19

2 Answers2

0

enter image description here

$\vec V_{reflected} =\vec V_{incident} -2\vec n(\vec V_{incident} \cdot \vec n)$

K. Rmth
  • 1,757
-1

I also had this problem. you can do $\vec{v} \times \vec{p}$ and consider $x$ and $y$ coordinates only.

In fact for any $\vec{v}=(x,y,0)$ and $\vec{p}=(0,0,1)$ then $\vec{v} \times \vec{p}=\begin{bmatrix}\vec{i} & \vec{j} & \vec{k}\\x & y & z \\ 0 & 0 & 1\end{bmatrix} = y\vec{i}-x\vec{j}+0\vec{k}=(y,-x)$

That implies that the normal vector $\vec{n}=(\vec{V}y, -\vec{V}x)$

Carlos Afonso
  • 353
  • 1
    The OP used $\vec v$ for the velocity of the ball and $\vec p$ for the position of the center of the rectangle. Those two things do not determine the direction of the normal vector at all, so it is really unclear what you think you are doing with the formulas in this answer. – David K Jul 29 '16 at 15:52
  • This would only be helpful in 3D – gen-ℤ ready to perish Nov 24 '20 at 06:37